A fixed mass of helium gas is made to undergo a process in which its pressure varies linearly from 1kPa to 2kPa, in relation to its volume as the latter varies from 0.2m3 to 0.4m3. The heat absorbed by the gas will be
300J
900J
1200J
1500J
The correct Answer is:C
To solve the problem of calculating the heat absorbed by a fixed mass of helium gas undergoing a linear pressure-volume process, we can follow these steps:
Step 1: Understand the Process
We have a fixed mass of helium gas with pressure varying from P1=1kPa to P2=2kPa and volume varying from V1=0.2m3 to V2=0.4m3.
Step 2: Draw the PV Diagram
Plot the points on a Pressure-Volume (PV) diagram. The initial point (1) is at (0.2 m³, 1 kPa) and the final point (2) is at (0.4 m³, 2 kPa). The line connecting these points represents the process.
Step 3: Calculate Change in Internal Energy
Using the formula for change in internal energy for an ideal gas:
ΔU=nCvΔT
We can also express it in terms of pressure and volume:
ΔU=P2V2−P1V1γ−1
Where γ=CpCv for helium (a monatomic gas) is 53.
Substituting the values:
ΔU=(2kPa×0.4m3)−(1kPa×0.2m3)53−1
Calculating:
ΔU=(0.8−0.2)kPa m323=0.6kPa m323=0.9kJ=900J
Step 4: Calculate Work Done
The work done by the gas during this process can be calculated as the area under the PV curve, which forms a trapezium:
W=12×(P1+P2)×(V2−V1)
Substituting the values:
W=12×(1kPa+2kPa)×(0.4m3−0.2m3)
Calculating:
W=12×3kPa×0.2m3=0.3kJ=300J
Step 5: Apply the First Law of Thermodynamics
According to the first law of thermodynamics:
Q=ΔU+W
Substituting the values we found:
Q=900J+300J=1200J
Conclusion
The heat absorbed by the gas is:
1200J
We have a fixed mass of helium gas with pressure varying from P1=1kPa to P2=2kPa and volume varying from V1=0.2m3 to V2=0.4m3.
Plot the points on a Pressure-Volume (PV) diagram. The initial point (1) is at (0.2 m³, 1 kPa) and the final point (2) is at (0.4 m³, 2 kPa). The line connecting these points represents the process.
Using the formula for change in internal energy for an ideal gas:
ΔU=nCvΔT
We can also express it in terms of pressure and volume:
ΔU=P2V2−P1V1γ−1
Where γ=CpCv for helium (a monatomic gas) is 53.
ΔU=(2kPa×0.4m3)−(1kPa×0.2m3)53−1
Calculating:
ΔU=(0.8−0.2)kPa m323=0.6kPa m323=0.9kJ=900J
The work done by the gas during this process can be calculated as the area under the PV curve, which forms a trapezium:
W=12×(P1+P2)×(V2−V1)
Substituting the values:
W=12×(1kPa+2kPa)×(0.4m3−0.2m3)
Calculating:
W=12×3kPa×0.2m3=0.3kJ=300J
According to the first law of thermodynamics:
Q=ΔU+W
Substituting the values we found:
Q=900J+300J=1200J
The heat absorbed by the gas is:
1200J
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Multiple Corrects
28 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning
6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Subjective
22 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
For an ideal gas
View SolutionStatement I: A quasi -static process is so called bacause it is a sudden and large change of the system.
Statement II: An adiabatic process is not quasi- static because it is a sudden and large change of the system.
View SolutionFive grams of helium having rms speed of molecules 1000m/s and 24g of oxygen having rms speed of 1000m/s are introduced into a thermally isolated vessel. Find the rms speeds of helium and oxygen individually when thermal equilibrium is attained. Neglect the heat capacity of vessel.
View SolutionOne mole of an ideal monatomic gas undergoes a linear process from A to B , in which is pressure P and its volume V change as shown in figure .
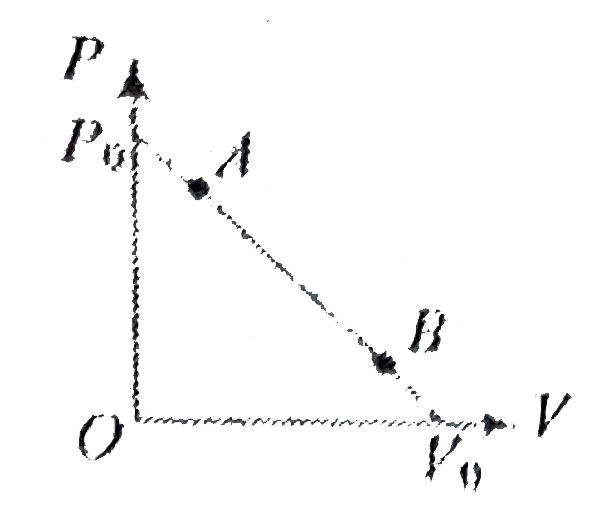
The absolute temperature T versus volume V for the given process is
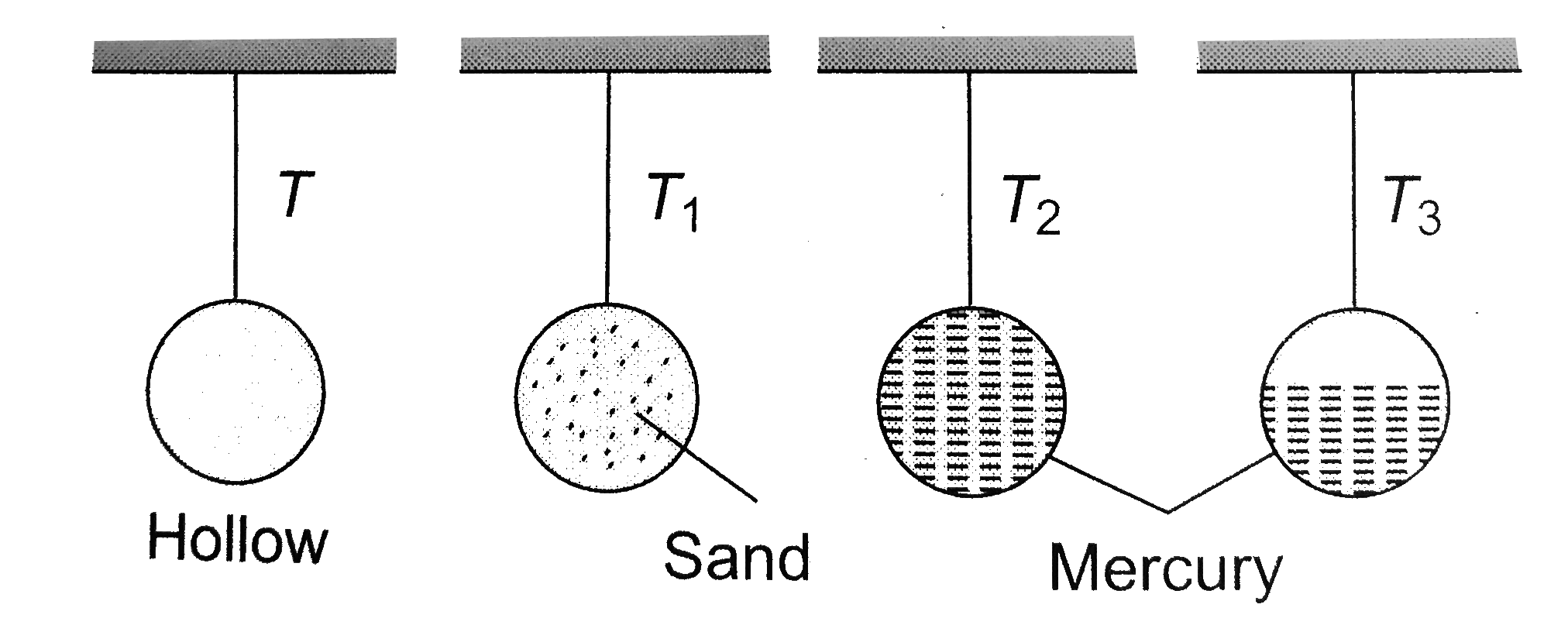
View SolutionThe period of a simple pendulum whose bob is hollow metallic sphere is T. The period is T1 when the bob is filled with sand, T2 where it is filled with mercury and T3 when it is half filled with mercury Which of the following is true?
View SolutionA gas is initinaly at a pressure of 100 kPa and its volume is 2.0m3. Its pressure is kept constant and the volume is changed from 2.0m3→2.53. Its volume is now kept constant and the pressure is increased from 100 lPa to 200 kPa. The gas is brought back to its initial state, the pressure varying linearly with its volume. (a) whether the heat is supplied to or exterted from the gas in the complete cycle ? (b) how much heat was supplied or extracted ?
View SolutionA fixed mass of helium gas is made to undergo a process in which its pressure varies linearly from 1 kPa to 2 kPa , in relation to its volume as the latter varies from 0.2 m^(3) to 0.4 m^(3) . The heat absorbed by the gas will be
View SolutionA certain balloon maintains an internal gas pressure of P0=100kPa until the volume reaches V0=20m3. Beyond a volume of 20m3, the internal pressure varies as P=P0+2k(V−V0)2 where P is in kPa. V is n m3 and k is a constant (k=1kPa/m3). Initially the balloon contains helium gas at 20∘C, 100kPa with a 15m3 volume. The balloon is then heated until the volume becomes 25m2 and the pressure is 159 kPa. Assume ideal gas behaviour for helium. The work done by the balloon for the entire process in kJ is
View SolutionA gas is initially at a pressure of 100 kPa and its volume is 2.0m3. Its pressure is kept constant and the volume is changes from 2.0m3 to 2.5m3. Its volume is now kept constant and the pressure is increased from 100 kPa to 200 kPa. The gas is brought back to its initial state, the pressure verying linearly with its volume. Whether the heat is supplied to or extracted from the gas in the complete cycle?
View SolutionThe mass of 2.24×10−3m3 of a gas is 4.4 g at 273.15 K and 101.325 Kpa pressure. The gas may be
View Solution2 moles of helium gas expanded isothermally and irreversibly at 27^(@)C from volume 1 dm^(3) to 1 m^(3) at constant pressure of 100 kPa. Calculate the work done.
View SolutionThe mass of 2.24xx10^(-3)m^(3) of a gas is 4.4 g at 273.15 K and 101.325 kPa pressure. The gas may be
View SolutionBoyle's law states that when a sample of gas is compressed at a constant temperature , the pressure of the gas is inversely proportional to the volume of the gas . If a sample of air occupies 0.106m3 at 25∘C , the pressure is 50 kPa (kilopascals). Find the new pressure , in kPa, if the temperature remains constant and the sample expands to a volume of 0.3m3.
View SolutionIn a cyclic process initially a gas is at 10^5 Pa pressure and its volume is 2 m^3 . First it undergoes an isobaric expansion to increase its volume to 2.5 m^3 . The in an isochoric process its pressure is doubled. Now the gas is brought back to its initial state by changing the pressure of gas linearly with its volume. Find the total amount of heat supplied to the gas in the process.
View SolutionThe pressure of an ideal gas varies with volume as P= aV, where a is a constant. One mole of the gas is allowed to undergo expansion such that its volume becomes ‘m’ times its initial volume. The work done by the gas in the process is
View Solution

