A μ−meson("charge -e , mass = 207 m, where m is mass of electron") can be captured by a proton to form a hydrogen - like ''mesic'' atom. Calculate the radius of the first Bohr orbit , the binding energy and the wavelength of the line in the Lyman series for such an atom. The mass of the proton is 1836 times the mass of the electron. The radius of the first Bohr orbit and the binding energy of hydrogen are 0.529Å and 13.6eV , repectively. TakeR = 1.67 xx 109678 cm^(-1)
The correct Answer is:0.002844Å,2530eV,653.6Å
To solve the problem of calculating the radius of the first Bohr orbit, the binding energy, and the wavelength of the line in the Lyman series for a mesic atom formed by a mu-meson and a proton, we will follow these steps:
Step 1: Calculate the Reduced Mass
The reduced mass (μ) of the system can be calculated using the formula:
μ=m1m2m1+m2
where m1 is the mass of the mu-meson and m2 is the mass of the proton.
Given:
- Mass of mu-meson = 207m (where m is the mass of the electron)
- Mass of proton = 1836m
Substituting the values:
μ=(207m)(1836m)207m+1836m=(207)(1836)m22043m=380772m22043m≈186m
Step 2: Calculate the Radius of the First Bohr Orbit
The radius of the first Bohr orbit (r) can be calculated using the formula:
r=r0meμ
where r0 is the radius of the first Bohr orbit for hydrogen, which is given as 0.529Å.
Substituting the values:
r=0.529Å⋅m186m=0.529186Å≈0.00284Å
Step 3: Calculate the Binding Energy
The binding energy (E) can be calculated using the formula:
E=−μe42ℏ2R
where R is the Rydberg constant given as 1.67×109cm−1.
Using the known binding energy of hydrogen (EH=13.6eV):
E=EH⋅μme=13.6eV⋅186mm=13.6×186eV≈2530.56eV
Step 4: Calculate the Wavelength of the Line in the Lyman Series
For the Lyman series, the wavelength (λ) can be calculated using the formula:
1λ=Rμ(1−1n2)
For the first line in the Lyman series, n=2:
1λ=Rμ(1−122)=Rμ(1−14)=Rμ⋅34
Substituting the values:
1λ=(1.67×109cm−1)⋅(186m)⋅34
Calculating λ:
λ=43⋅1Rμ≈43⋅11.67×109⋅186≈653.6Å
Final Answers
- Radius of the first Bohr orbit: 0.00284Å
- Binding energy: −2530.56eV
- Wavelength of the line in the Lyman series: 653.6Å
The reduced mass (μ) of the system can be calculated using the formula:
μ=m1m2m1+m2
where m1 is the mass of the mu-meson and m2 is the mass of the proton.
- Mass of mu-meson = 207m (where m is the mass of the electron)
- Mass of proton = 1836m
μ=(207m)(1836m)207m+1836m=(207)(1836)m22043m=380772m22043m≈186m
The radius of the first Bohr orbit (r) can be calculated using the formula:
r=r0meμ
where r0 is the radius of the first Bohr orbit for hydrogen, which is given as 0.529Å.
r=0.529Å⋅m186m=0.529186Å≈0.00284Å
The binding energy (E) can be calculated using the formula:
E=−μe42ℏ2R
where R is the Rydberg constant given as 1.67×109cm−1.
E=EH⋅μme=13.6eV⋅186mm=13.6×186eV≈2530.56eV
For the Lyman series, the wavelength (λ) can be calculated using the formula:
1λ=Rμ(1−1n2)
For the first line in the Lyman series, n=2:
1λ=Rμ(1−122)=Rμ(1−14)=Rμ⋅34
1λ=(1.67×109cm−1)⋅(186m)⋅34
Calculating λ:
λ=43⋅1Rμ≈43⋅11.67×109⋅186≈653.6Å
- Radius of the first Bohr orbit: 0.00284Å
- Binding energy: −2530.56eV
- Wavelength of the line in the Lyman series: 653.6Å
Topper's Solved these Questions
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Single Correct
187 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Multiple Correct
13 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Exercise 4.2
12 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Single Correct
10 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
Similar Questions
if the wavelength of the first line of the balmer series of hydrogen is 6561Å, the wavelength of the second line of the series should be
View SolutionWhich of the following statements are true?
View Solutionstate True or False for the given statement a. X-ray are electromagnetic waves because these are producted by the deceleration of fast moving electron .
b. X-ray are electromagnetic waves because these produce line spectrum.
c. the cut-off wavelength depends on the target material .
d. The intensity of Kα transition is more probable then of Kβ
transition.
e. Frequency of Kα radiation is more than that of Kβ.
View SolutionThe rms current in an AC circuit is 2A. If the wattless current be √3A , what is the power factor of the circuit?
View SolutionEach capacitance shown in is in μF. Find the charge on 6μF.
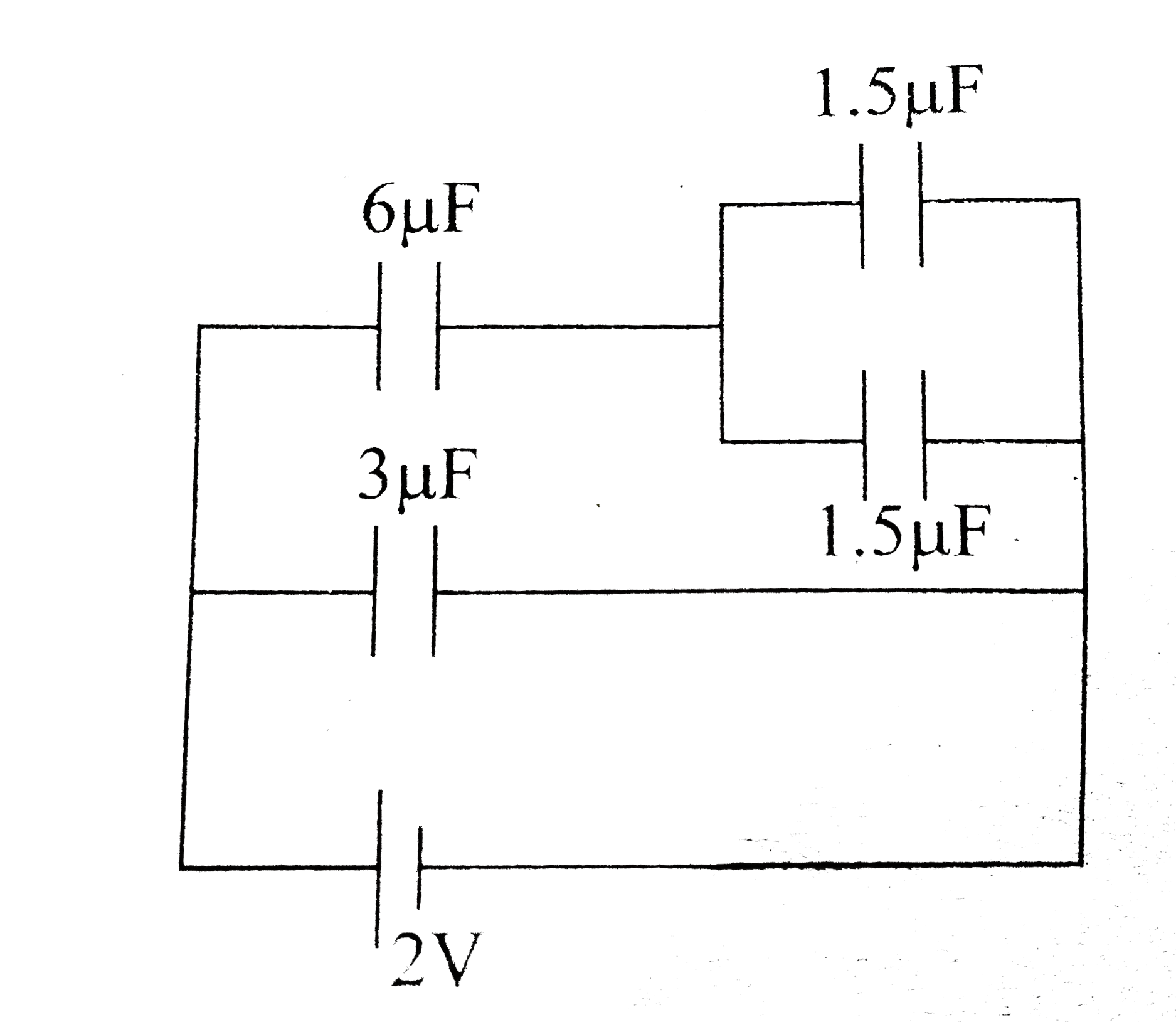 .
.
View SolutionA μ−meson("charge -e , mass = 207 m,wheremismassofe≤ctron) can be captured by a proton to form a hydrogen - like ''mesic'' atom. Calculate the radius of the first Bohr orbit , the binding energy and the wavelength of the line in the Lyman series for such an atom. The mass of the proton is 1836 times the mass of the electron. The radius of the first Bohr orbit and the binding energy of hydrogen are 0.529Å and 13.6eV , repectively. TakeR = 1.67 xx 109678 cm^(-1)
View SolutionCalculate the separation between the particles of a system in the ground state, the corresponding binding energy, and the wavelength of the first line of Lyman series,if such a system is (a) a mesonic hydrogen atom whose nucleus is a proton (in a mesonic atom an electron is replaced by a meson whose charge is the same and mass is 207 si that of an electron), (b) a positronium consisting of an electron and positron revolving around their common centre of masses.
View SolutionThe radius of first Bohr orbit of hydrogen atom is 0.53Å. Then the radius of first Bohr-orbit of mesnoic atom (negative meson has mass 207 times that of electron but same charge) is:
View SolutionCalculate the separation between particles, the binding energy and the wave-length of the first line of the Kyman series of a mesonic hydrogen (i.e an atom consisting of a proton +a revolving meson in place of an electron). Mass of a meson =207 times mass of electron and charge of meson = charge of electron.
View SolutionThe mass of a proton is 1836 times more than the mass of an electron. It a sub-atomic of mass (m) 207 times the mass of electron is captured by the nucleus, then the first ionization potential of H :
View Solutionप्रथम बोहर-त्रिज्या और म्यूओनिक हाइड्रोजन परमाणु [अर्थात कोई परमाणु जिसमें लगभग 207 me द्रव्यमान का ऋणावेशित म्यूऑन (μ−) प्रोटॉन के चारों ओर घूमता है] कि निम्नतम अवस्था ऊर्जा तो प्राप्त करने का परिकलन कीजिए।
View SolutionIf m and e are the mass and charge of the revolving electron in the orbit of radius r for hydrogen atom, the total energy of the revolving electron will be :
View Solutionम्युऑनिक हाइड्रोजन परमाणु में ऋणावेशित म्यूऑन (μ−) जिसका द्रव्यमान इलेक्ट्रॉन के द्रव्यमान का 207 गुना होता है, प्रोटॉन के चारो ओर परिक्रमण करता है। इस परमाणु के लिए प्रथम बोर त्रिज्या तथा निम्नतम ऊर्जा के मान प्राप्त करे। सामान्य हाइड्रोजन की निम्नतम कक्षा की त्रिज्या 5.3×10−11m और निम्नतम ऊर्जा −13.6eV ले ।
View SolutionObtain the first Bohr radius and the ground state energy of a muonic hydrogen atom (I.e ., an atom in which negatively charged muon ( mu^(-)) of mass about 207 m_e orbits around a proton).
View SolutionThe mass of electron is 1836 times that of proton.
View Solution

