A thermally insulated chamber of volume 2V0 is divided by a frictionless piston of area S into two equal parts A and B Part A has an ideal gas at pressure p0 and temperature T0 and in part B is vacuum. A massless spring of force constant K is connected with piston and the wall of the container as shown. Initially spring is unstretched. Gas in chamber A is allowed to expand. Let in equilibrium spring is compressed by x0. Then

final pressure of the gas is Kx0S
work done by the gas is 12Kx20
change in internal energy of the gas is 12Kx20
temperature of the gas is decreased
The correct Answer is:A, B, C, D
Equilibrium of piston gives PS=Kx0
P=Kx0S
Since the chamber is thermally insulated, ΔQ=0
∴ Elastic PE of spring = Work done by gas
or, Work done by gas =12Kx20
This work is done at the expense of internal energy of the gas. Therefore, internal energy of the gas is decreased by (1/2)Kx20.

Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Assertion-Reasoning
Explore 6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Comprehension
Explore 56 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Single Correct
Explore 140 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Single correct anwer type
Explore 14 Videos
Similar Questions
Statement I: A quasi -static process is so called bacause it is a sudden and large change of the system.
Statement II: An adiabatic process is not quasi- static because it is a sudden and large change of the system.
View SolutionA fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal. Find pressure at C
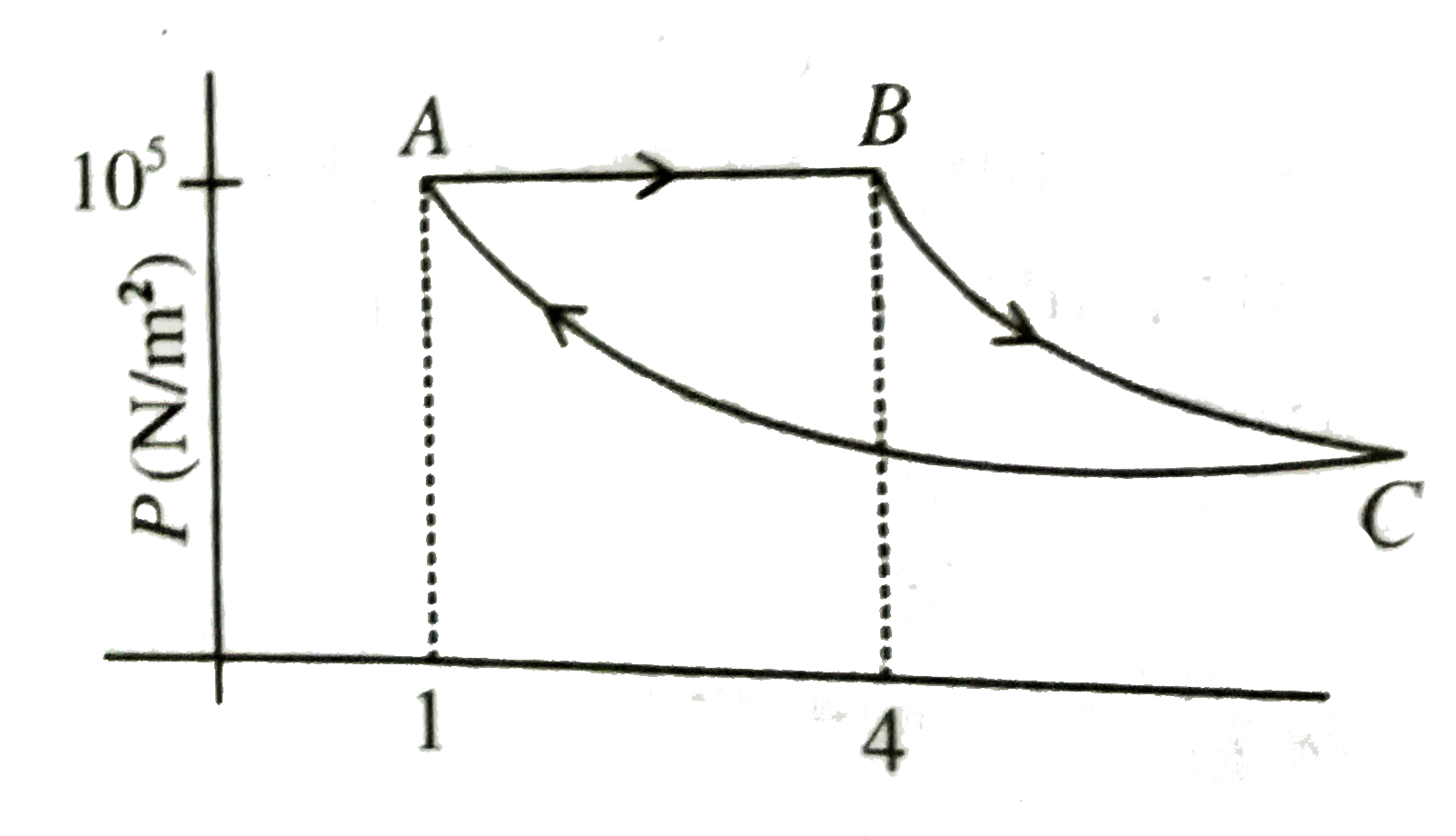
.
View SolutionThe temperature of a gas is raised while its volume remains constant, the pressure exerted by the gas on the walls of the container increases because its molecules
View SolutionOne mole of an ideal monatomic gas undergoes a linear process from A to B , in which is pressure P and its volume V change as shown in figure .
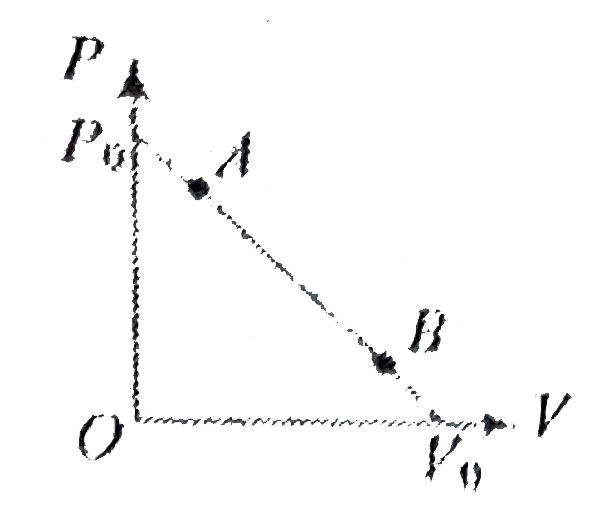
The absolute temperature T versus volume V for the given process is
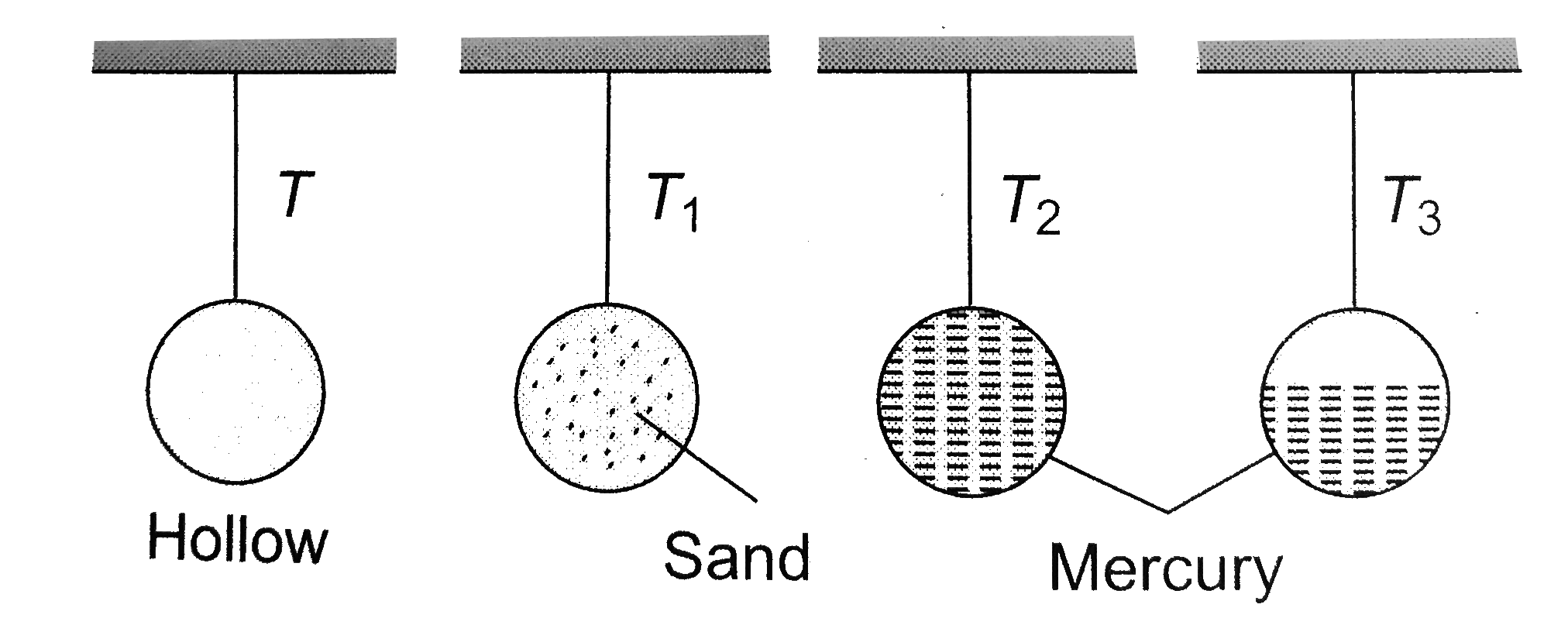
View SolutionThe period of a simple pendulum whose bob is hollow metallic sphere is T. The period is T1 when the bob is filled with sand, T2 where it is filled with mercury and T3 when it is half filled with mercury Which of the following is true?
View SolutionA thermally insulated chamber of volume 2V0 is divided by a frictionless piston of area S into two equal part A and B. Part A has an ideal gas at pressrue P0 and temperature T0 and part B is vacuum. A massless spring of force constant K is connected with the piston and the wall of the container as shown. Initially the spring is unstretched. The gas inside chamber A is allowed to expand. Let in equilibrium the spring be compressed by x0. Then

View SolutionIn the arrangement shown in Fig. gas is thermally insulated. An ideal gas is filled in the cylinder having pressure P_(0) (gt atmospheric pressure P_(0) ). The spring of force constant K is initially unstretched. The piston of mass m and area S is frictionless. In equilibrium, the piston rises up by distance x_(0) , then
View SolutionA cylindrical container is divided into three parts by two tight fitting pistons. The pistons are connected by a spring. The region between the pistons is vacuum and the other two parts have same number of moles of an ideal gas. Initially, both the gas chambers are at temperature T_(0) and the spring is compressed by 1 m. Length of both gas chambers is 1 m in this position. Now the temperature of the left and right chambers are raised to (4T_(0))/(3) and (5T_(0))/(3) respectively. Find the final compression in the spring in equilibrium. Assume that the pistons slide without friction
View SolutionConsider the adjacent figure. A piston divides a cylindrical container into two equal parts. The lets part contains 1 mole of helium gas and the right part contains two moles or oxygen gas. The initial temperatures and pressures of the gases in the left chamber are T_(0) and p_(0) and the right chamber are (T_(0))/(2) and p_(0) respectively as shown in the figure. The piston as well as the walls of the container are adiabatic. After removal of the piston, gases mix homoganeously and the final pressure becomes p=(4n)/(13)p_(0) . Find the value of n.
View SolutionOne mole of a monoatomic ideal gas occupies two champers of a cylinder partioned by means of a movable pision. The walls of the cylinder as well as the piston are thermal insulators. Initially equal amounts of gas fill both the chambers at (P0,V0,T0). A coil is burnt in the left chamber which absorbs heat and expands , pushing the piston to the right . The gas on the right chamber is compressed until to pressure becomes 32P0.
_S01_110_O01.png)
The final volume of left chamber is
View SolutionOne mole of a monoatomic ideal gas occupies two champers of a cylinder partioned by means of a movable pision. The walls of the cylinder as well as the piston are thermal insulators. Initially equal amounts of gas fill both the chambers at (P0,V0,T0). A coil is burnt in the left chamber which absorbs heat and expands , pushing the piston to the right . The gas on the right chamber is compressed until to pressure becomes 32P0.
_S01_111_O01.png)
The work done on the gas in the right chamber is
View SolutionA cylindrical adiabatic container of total volume 2V0 divided into two equal parts by a conducting piston which is free to move as shown in figure. Each part containing identical gas at pressure P0. Initially temperature of left and right part is 4T0andT0 respectively. An external force is applied on the piston of area 'A' to keep the piston at rest. The value of external force required when thermal equilibrium is reached is.
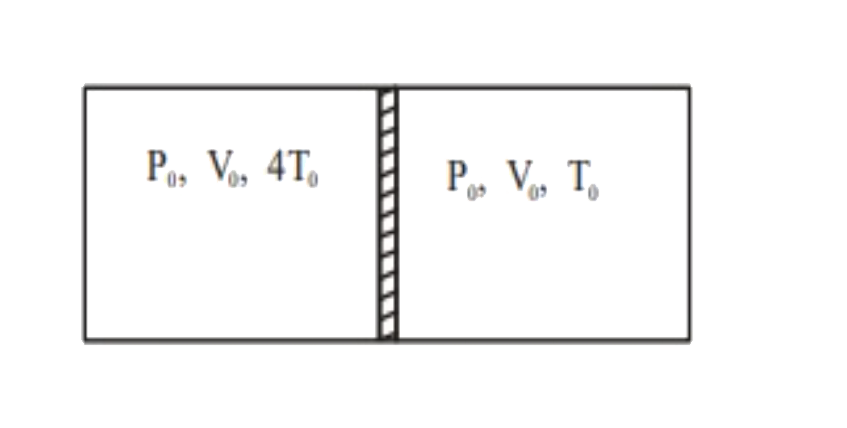
View SolutionA thermally insulated chamber of volume 2V_(0) is divided by a frictionless piston of area S into two equal part A and B . Part A has an ideal gas at pressrue P_(0) and temperature T_(0) and part B is vacuum. A massless spring of force constant K is connected with the piston and the wall of the container as shown. Initially the spring is unstretched. The gas inside chamber A is allowed to expand. Let in equilibrium the spring be compressed by x_(0) . Then
View SolutionConsider the adjacent figure. A piston divides a cylindrical container into two equal parts. The lets part contains 1 mole of helium gas and the right part contains two moles or oxygen gas. The initial temperatures and pressures of the gases in the left chamber are T_(0) and p_(0) and the right chamber are (T_(0))/(2) and p_(0) respectively as shown in the figure. The piston as well as the walls of the container are adiabatic. After removal of the piston, gases mix homoganeously and the final pressure becomes p=(4n)/(13)p_(0) . Find the value of n.
View SolutionConsider the adjacent figure. A piston divides a cylindrical container into two equal parts. The lets part contains 1 mole of helium gas and the right part contains two moles or oxygen gas. The initial temperatures and pressures of the gases in the left chamber are T0 and p0 and the right chamber are T02 and p0 respectively as shown in the figure. The piston as well as the walls of the container are adiabatic. After removal of the piston, gases mix homoganeously and the final pressure becomes p=4n13p0. Find the value of n.
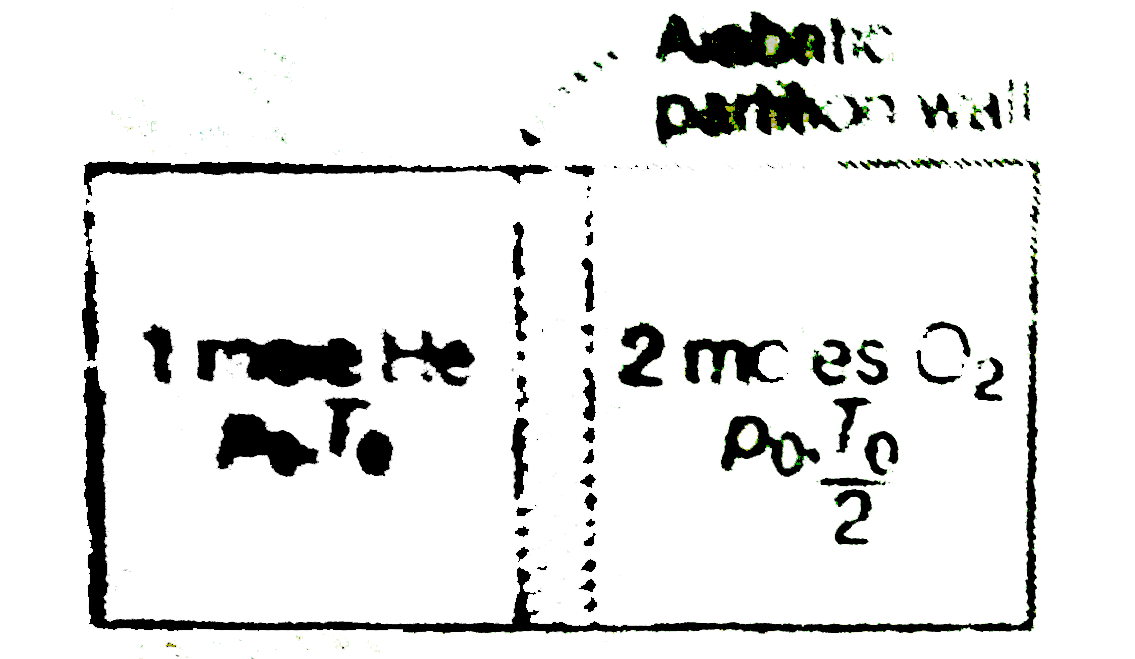
View SolutionA thermally insulated chamber of volume 2V0 is divided by a frictionless piston of area S into two equal part A and B. Part A has an ideal gas at pressrue P0 and temperature T0 and part B is vacuum. A massless spring of force constant K is connected with the piston and the wall of the container as shown. Initially the spring is unstretched. The gas inside chamber A is allowed to expand. Let in equilibrium the spring be compressed by x0. Then

View Solution
