An isosceles triangles is formed with a thin rod of length l1 and coefficient of linear expansion α1, as the base and two thin rods each of length l2 and coefficient of linear expansion α2 as the two sides. The distance between the apex and the midpoint of the base remain unchanged as the temperature is varied. the ratio of lengths l1l2 is

L1L2=α2α1
L1L2=√α2α1
L1L2=2α2α1
L1L2=2√α2α1
The correct Answer is:D
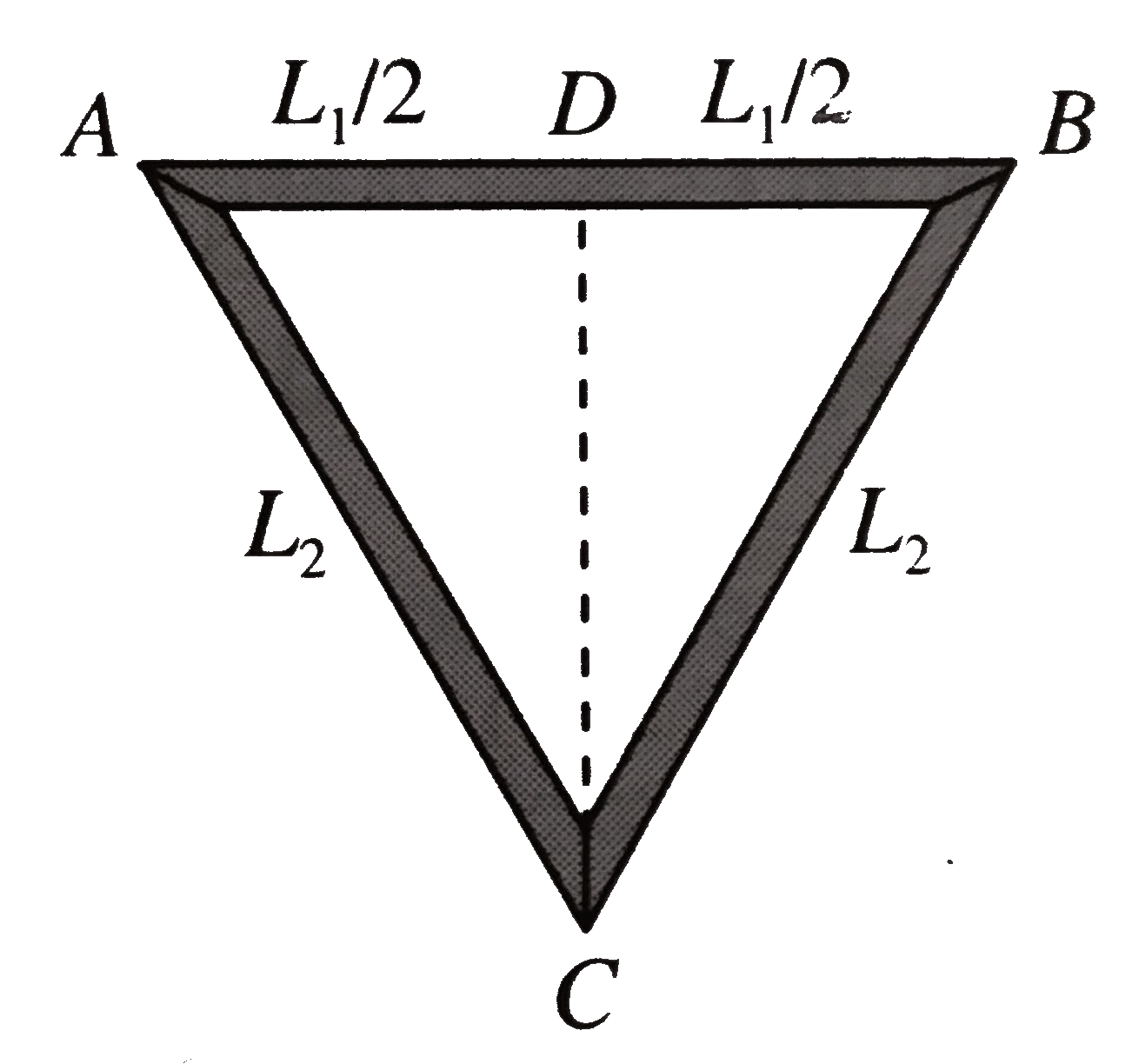
The apex of the isosceles Delta to remain at a constant distance form the knife edge. Thus, DC should remain constant before and after heating
Before expansion: In Delta ADC
(DC)2=L22−(L12)2 .(i)
After expansion:
(DC)2=[L2(1+α2t]2−[L12(1+α1t)]2 ..(ii)
Equating Eqs. (i) and (ii) we get
L22−(L12)2=[L2(1+α2t)]2−[L12(1+α1t)]2
L22−L214=L22+L22×2α2×t−L214−L214×2α1×t
(neglecting higher terms)
⇒L214(2α1t)=L22(2α2t)⇒L1L2=2√α2α1
Topper's Solved these Questions
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Multiple Correct
Explore 25 Videos
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Comprehension
Explore 30 Videos
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Subjective
Explore 25 Videos
- BASIC MATHEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:BASIC MATHEMATICSExercise:Exercise 2.6
Explore 20 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
Due to thermal expansion with rise in temperature:
View SolutionA body cools in a surrounding of constant temperature 30∘C Its heat capacity is 2J/∘C. Initial temperature of cooling is valid. The body of mass 1 kg cools to 38∘C in 10 min
When the body temperature has reached 38∘C, it is heated again so that it reaches 40∘C in 10 min. The heat required from a heater by the body is
View SolutionA lead ball at 25∘C is dropped from a height of 2 km. It is heated due to air resistance and it is assumed that all of its kinetic energy is used in increasing the temperature of ball. Find the final temperature of the ball.
View SolutionThe displacement of a particle is given by y=(6t2+3t+4)m, where t is in seconds. Calculate the instantaneous speed of the particle.
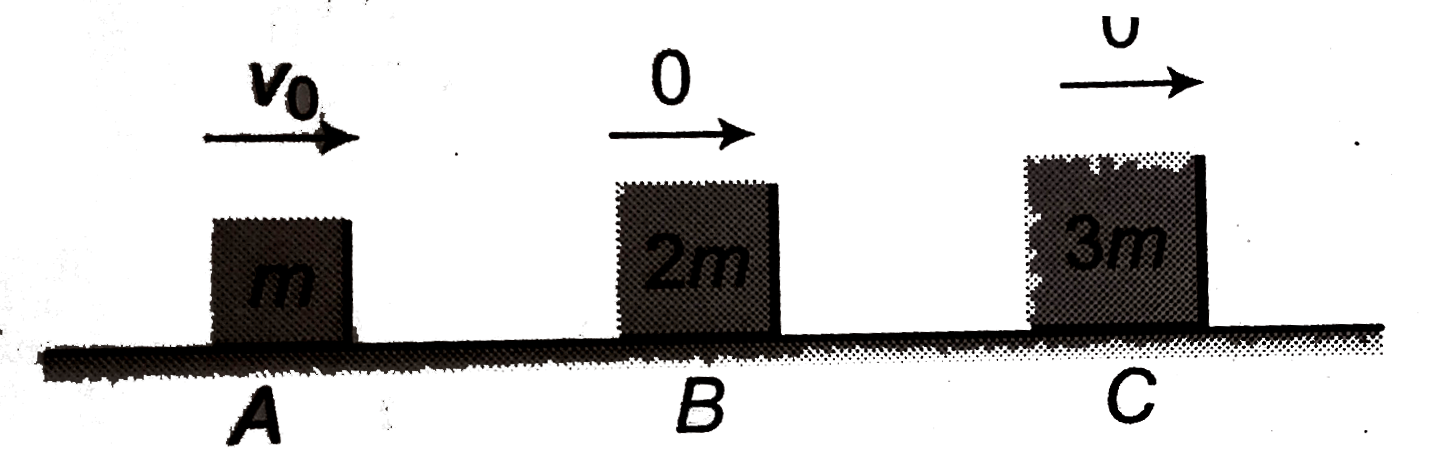
View SolutionThree objects A ,B and C are kept in a straight line on a smooth horizontal surface. These have masses m, 2m and 3m , respectively . The head - on elastic collision takes place between A and B and then B makes completely inelastic collision with C. All motions occur on the same straight line. The final speed of C will be
View SolutionAn isosceles triangle is formed with a thin rod of length l1 and coefficient of linear expansion α1, as the base and two thin rods each of length l2 and coefficient of linear expansion α2 as the two sides. The distance between the apex and the midpoint of the base remain unchanged as the temperature is varied. the ratio of lengths l1l2 is

View SolutionA composite bar of length L = L_(1) + L_(2) is made up from a rod of material 1 and of length L_(1) attached to a rod of material 2 and of length L_(2) as shown. If alpha_(1) and alpha_(2) are their respective coefficient of linear expansion, then equivalent coefficient of linear expansion for the composite rod is
View SolutionTwo rods of length l_(1) and l_(2) are made of material whose coefficient of linear expansion are alpha_(1) and alpha_(2) , respectively. The difference between their lengths will be independent of temperatiure if l_(1)//l_(2) is to
View SolutionTwo rods of lengths L1 and L2 are welded together to make a composite rod of length (L1+L2). If the coefficient of linear expansion of the materials of the rod are α1 and α2 respectively. The effective coefficient of linear expansion of the composite rod is
View SolutionTwo rods having length l1 and l2, made of materials with the linear coefficient of expansion α1 and α2 were welded togther. The equivalent coefficients of linear expansion for the obtained rod:-

View SolutionTwo rods each of length L2 and coefficient of linear expansion α2 each are connected freely to a third rod of length L1 and coefficient of expansion α1 to form an isoscles triangle. The arrangement is supported on a knife-edge at the midpoint of L1 which is horizontal. what relation must exist between L1 and L2 so that the apex of the isoscles triangle is to remain at a constant height from the knife edge as the temperature changes ?
View SolutionTwo metal rods of lengths L_(1) and L_(2) and coefficients of linear expansion alpha_(1) and alpha_(2) respectively are welded together to make a composite rod of length (L_(1)+L_(2)) at 0^(@)C. Find the effective coefficient of linear expansion of the composite rod.
View SolutionTwo rods of length L1 and L2 are made of materials of coefficients of linear expansions α1 an α2 respectively such that L1α1=L2α2. The temperature of the rods is increased by ΔT and correspondingly the change in their respective lengths be ΔL1 and ΔL2
View SolutionTwo rods of different metals of coefficient of linear expansion α1 and α2 and initial length l1 and l2 respectively are heated to the same temperature. Find relation in α1,α2,l1 and l2such that difference between their lengths remain constant.
View SolutionTwo rods, each of coefficient of linear expansion alpha_(2) and length l_(2) , form the two sides of an isosceles triangle and the base is formed by another rod of length l_(1) and coefficient of linear expansion alpha_(1). The base is fixed horizontally at its mid-point. What should be the relationship between l_(1) " and " l_(2) so that the distance of the vertex from the mid-point of the base, does not change for any increase in temperature?
View Solution
