Describe Young's double slitexperiment to produce interference pattern due to a monochromatic source of light. Deduce the expression for the fringe width.
Simplest experiment to show interference of light is Young's double slit experiment : δ is a narrow slit (of width about 1 mn) illuminated by a monochromatic source of light. At a suitable distance (≈10mm) form δ, two slits S1andS2 are placed parallel to S. When a screen is placed at a large distance (about 2m) from the slit S1andS2, alternate dark and bright bands appear on the screen. These are the interference bands or fringas. The bond disappear when either slit is covered.
Explanation : According to Huygen's pricipal, the monochromatic source of light illuminating the slit S tends out spherical wavefront.
The two waves of same amplitude and same freqency superimpose on each other.
Dark fringes appear on the screen when the crest of one wave falls on the trough of other and they neutralise the effect of each other.
Bright fringes appear on the screen when the crest of one wave coincides with the crest of other and they reinforce each other.
Expression for the fringe width :
Let d= distance between slits S1andS2
D= distance of screen from two slits
and x = distance between the central maxima O and observation point P.


Light waves spread out from S and fall on both S1andS2. The spherical waves emanating from S1andS2 will produce interference frings on the screen MN.
In right ΔS1AP, we have,
(S1P)2=(S1A)2+(AP)2
S1P=√D2+(x−d2)2=
⎷D2⎡⎢
⎢
⎢⎣1+(x−d2)2D2⎤⎥
⎥
⎥⎦
S1P=D⎡⎢
⎢
⎢⎣1+(x−d2)2D2⎤⎥
⎥
⎥⎦=D+(x−d2)22D
Similarly S2P=D+(x+d2)22D
Hence, path difference =S2P−S1P
=D+(x+d2)22D−D−(x−d2)22D=12D[x2+d24+xd−x2−d24+xd]
=12D.2xd=xdD.
Now the intesity at point P is maximum or minimum according as the path difference is an integral multiple of wavelength or an odd intefral multiple of half wavelength.
(i) For Brigth fringe (constructive interference) : We will have constructive interference resulting in a bright fringe when path difference =nλ
xdD=nλ⇒x=nλDd
∴n=nλDd
where, n=0±1±2...
Since, the separation between the centres of two consecutive bright fringes is called fringe width. It is denoted by β
∴ Fringe width, β=xn+1−xn.
β=(m+1)λDdnλDd=λDd(n+1−n)
∴β=λDd
(ii) For Dark fringe (destructive interference): We will have destructive interference resulting in a dark fringe when path difference
=(2n+1)λ2
xdD=(2n+1)λ2⇒x=(2n+1)λD2d
∴xn=(2n+1)λD2d,
where, n=0,±1,±2,...
Fringe width β=xn+1−xn
=[2(n+1)+1]λD2d−(2n+1)λD2d=(2n+2+1−2n−1)λD2d=2λD2d
∴β=λDd
Hence, all bright and dark fringes are of equal width.
Observations :
(i) Fringe width is directly proportional to the wavalength of light i.e. βαλ.
(ii) Fringe width is inversely proportional to the distance between screen and two sourves i.e. βα1d.
(iii) Fringe width is directly proportional to the distance between screen and two sources i.e. βαD
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET-II, DELHI BOARD
8 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET-III, DELHI BOARD
8 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET -III
6 Videos
- SAMPLE PAPER 2019BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
The susceptibility of a magnetic material is 1⋅9×10−5. What type of material does it represent?
View SolutionA plane electromagnetic wave travels in vacuum along y-direction. What can you say about the direction of electric and magnetic field vectors?
View SolutionWhen light travels from a rarer to denser medium, it loses some speed. Does the reduction in speed imply a reduction in the energy carried by the light wave ?
View SolutionUsing Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
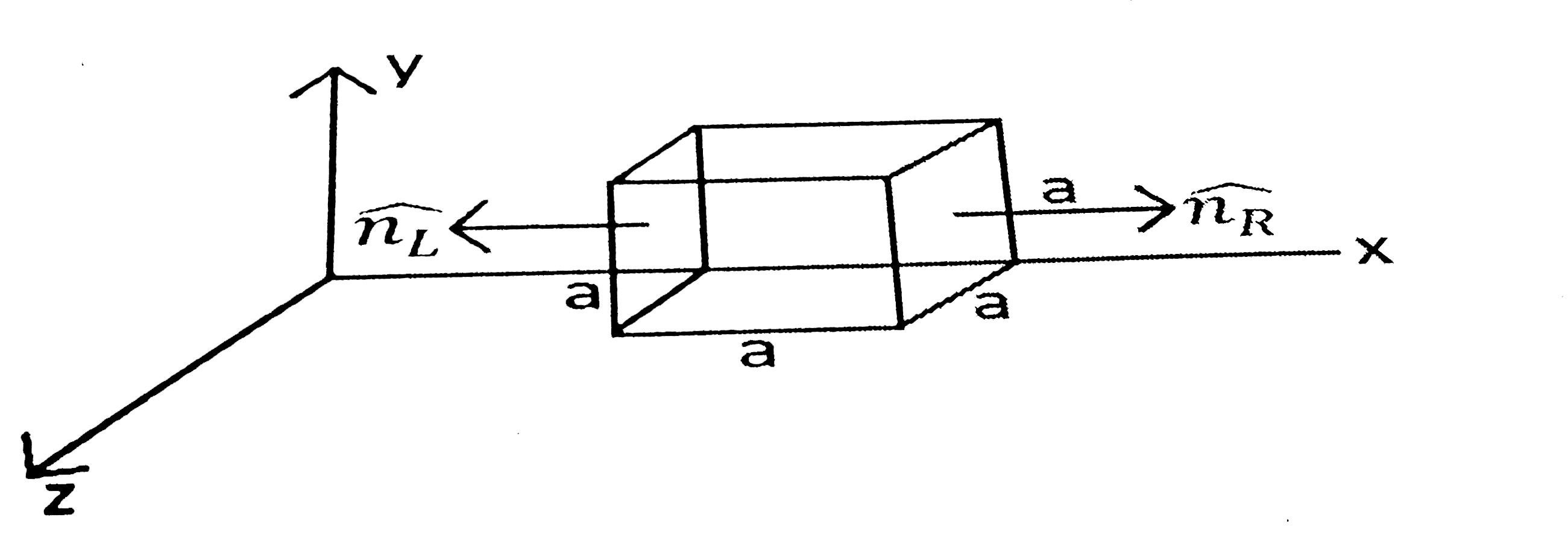
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.
View SolutionState the importance of coherent sources in the phenomenon of interference. In Young's double slit expet-ment to produce interference pattern obtain the conditions for constructive and destructive interference. Hence deduce the expression for the fringe width. How does the firinge width get affected, if the entire experimental apparatus of Young's is immersed in water ?
View Solutionएकवर्णी प्रकाश स्रोत के कारण व्यतिकरण प्रतिरूप उत्पन्न करने के लिए यंग के द्विस्लिट प्रयोग का वर्णन कीजिए। फ्रिंज चौड़ाई के लिए व्यंजक व्युत्पन्न कीजिए।
View SolutionObtain the expression for fringe width of interference fringes in Young's double slit experiment.
View SolutionObtain the expression for fringe width in the case of interference of light waves.
View SolutionWhat is the effect on the interference fringes in a Young's double-slit experiment if monochromatic source is replaced by source of white light ?
View SolutionDescribe Young's slit experiment to produce interference pattern due to a monochromatic source of light. Deduce the expression for the fringe width.
View SolutionState the importance of coherent sources in the phenomenon of interference. In Young's double-slit experiment to produce interference pattern, obtain the conditions for constructive and destructive interference. Hence, deduce the expression for the fringe width. How does the fringe width get affected, if the entire experimental apparatus of Young's is immersed in water ?
View SolutionObtain the expression for fringe width in the case of interference of light waves.
View SolutionIn Young's double slit experiment , describe briefly how bright and dark fringes are obtained on the screen kept in front of a double slit . Hence obtain the expression for the fringe width.
OR
Describe Young's double slit experiment to produce interference pattern due to a monochromatic source of light. Deduce the expression or the fringe width.
(b) The ratio of the intensities at the minima to the maxima in the Young's double slit experiment is 9:25 . Find the ratio of the widths of the two slits.
View SolutionDescribe Young's double slit experiment to produce interference pattern due to a monochromatic source of light. Deduce the expression for the fringe width.
View SolutionObtain the expression for fringe width in the case of interference of light waves.
View SolutionDerive an expression for fringe width in Young's double slit interference of light.
View Solution

