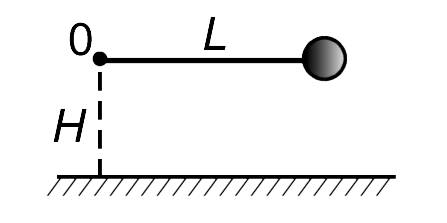
(i) O is a fixed peg at a height H above a perfectly inelastic smooth horizontal plane. A light inextensible string of length L(>H) has one end attached to O and the other end is attached to a heavy particle. The particle is held at the level of O with string horizontal and just taut and released from rest. Find the height of the particle above the plane when it comes to rest for the first time after the release.
(ii) The bob of a pendulum has mass m and the length of pendulum is l. It is initially at rest with the string vertical and the point of suspension at a height 2l above the floor. A particle P of mass
m2 moving horizontally along –ve x-direction with velocity √2gl collides with the bob and comes to rest. The bob swings and when it comes to rest for the first time, another particle Q of mass m moving horizontally along y direction collides with the bob and sticks to it. It is observed that the bob now moves in a horizontal circle.
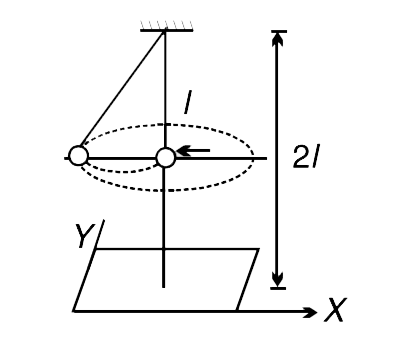
(a) Find tension in string just before the second collision.
(b) Find the height of the circular path above the floor.
(c) Find the time period of the circular motion.
(d) The string breaks during the circular motion at time t=0. At what time the bob will hit the floor ?
The correct Answer is:(i) H5L4
(ii) (a) 34mg
(b) 5l4
(c) 2π√3l4g
(d) √5l2g
Step by step video, text & image solution for (i) O is a fixed peg at a height H above a perfectly inelastic smooth horizontal plane. A light inextensible string of length L (gt H) has one end attached to O and the other end is attached to a heavy particle. The particle is held at the level of O with string horizontal and just taut and released from rest. Find the height of the particle above the plane when it comes to rest for the first time after the release. (ii) The bob of a pendulum has mass m and the length of pendulum is l. It is initially at rest with the string vertical and the point of suspension at a height 2l above the floor. A particle P of mass (m)/(2) moving horizontally along –ve x-direction with velocity sqrt(2gl) collides with the bob and comes to rest. The bob swings and when it comes to rest for the first time, another particle Q of mass m moving horizontally along y direction collides with the bob and sticks to it. It is observed that the bob now moves in a horizontal circle. (a) Find tension in string just before the second collision. (b) Find the height of the circular path above the floor. (c) Find the time period of the circular motion. (d) The string breaks during the circular motion at time t = 0. At what time the bob will hit the floor ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
(i) O is a fixed peg at a height H above a perfectly inelastic smooth horizontal plane. A light inextensible string of length L(>H) has one end attached to O and the other end is attached to a heavy particle. The particle is held at the level of O with string horizontal and just taut and released from rest. Find the height of the particle above the plane when it comes to rest for the first time after the release.

(ii) The bob of a pendulum has mass m and the length of pendulum is l. It is initially at rest with the string vertical and the point of suspension at a height 2l above the floor. A particle P of mass m2 moving horizontally along –ve x-direction with velocity √2gl collides with the bob and comes to rest. The bob swings and when it comes to rest for the first time, another particle Q of mass m moving horizontally along y direction collides with the bob and sticks to it. It is observed that the bob now moves in a horizontal circle.

(a) Find tension in string just before the second collision.
(b) Find the height of the circular path above the floor.
(c) Find the time period of the circular motion.
(d) The string breaks during the circular motion at time t=0. At what time the bob will hit the floor ?
View SolutionA heavy particle hanging from a string of length l is projected horizontally with speed √gl. Find the speed of the particle at the point where the tension in the string equals weight of the particle.
View Solution
Knowledge Check
A heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
A√31g,cos−1(3/2)B√1g3,cos−1(2/3)C√3g3,cos−1(2/3)D√gl3,cos−1(2/3)A heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizonally with speed √gl . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
A√glB√2glC√3glD√gl3One end of string of length l is connected to a particle on mass m and the other end is connected to a small peg on a smooth horizontal table. If the particle moves in circle with speed v the net force on the particle (directed toward centre) will be (T reprents the tension in the string):
AT+mv21BT−mv21CzeroDT
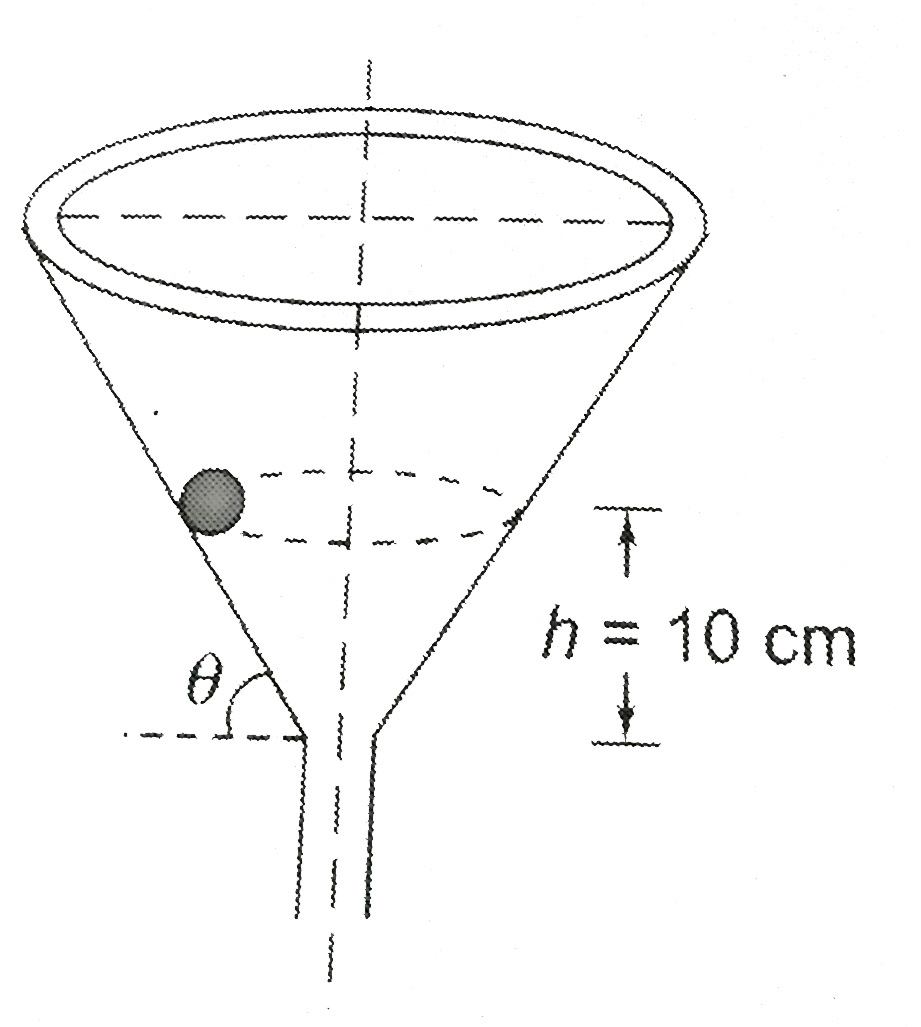
A particle describes a horizontal circle on smooth inner surface of a conical funnel as shown. If the height of the plane of the circle. Above the vertax is 10cm, find the speed of the paricle.
View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizonally with speed √gl . Find the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string is equal to the weight of the particle.
View SolutionA particle is fastened at the end of a string adis whirled in a verticle circle with the other end of het string being fixed. The motion of the particle is
View SolutionTwo particles of mass m each are attached to a light rod of length d, one at its centre and the other at a free end, The rod is fixed at the other end is rotated in a plane at an angular speed ω. Calculate the angular momentum of the particle at the end with respect to the particle at the centre
View SolutionA particle of mass 2m is connected by an inextensible string of length 1.2m to a ring of mass m which is free to slide on a horizontal smooth rod. Initially the ring and the particle are at the same level with the string taut. Both are then released simultaneously. The distance in meter moved by the ring when the string becomes veritcal is :-
View Solution

