Monochromatic light is incident on a glass prism of angle A. If the refractive index of the material of the prism is μ, a ray, incident at an angle θ, on the face AB would get transmitted through the face AC pf the prism provided.
 Solution in Gujrati
Solution in Gujrati
θ>sin−1[μsin(A−sin−1(1μ))]
θ<sin−1[μsin(A−sin−1(1μ))]
θ>cos−1[μsin(A+sin−1(1μ))]
θ<cos−1[μsin(A+sin−1(1μ))]
The correct Answer is:A
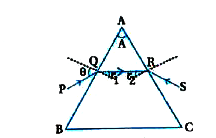
For transmission, r2<ic (Critical angle)
∴A−r1<ic (∵r1+r2=A)
∴sin(A−r1)<sinic
∴sin(A−r1)<1μ (∵sinic=1μ)
∴A−r1<sin−1(1μ)
∴r1>A−sin−1(1μ)
∴sinr1>sin[A−sin−1(1μ)](∵sinθ=μsinr1)
∴sinθμ>sin[A−sin−1(1μ)]
∴sinθ>μsin(A−sin−11μ)
∴θ>sin−1(μsin(A−sin−11μ))
Similar Questions
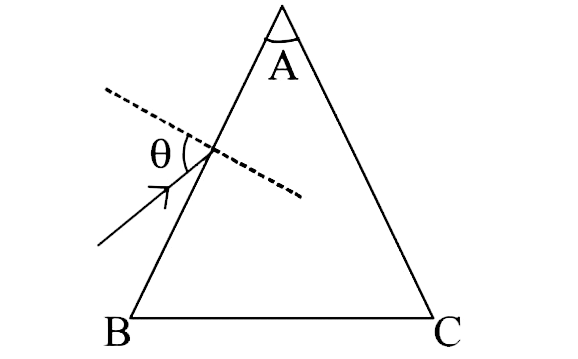
Monochromatic light is incident on a glass prism of angle A. If the refractive index of the material of the prism is μ, a ray, incident at an angle θ, on the face AB would get transmitted through the face AC of the prism provided:
View SolutionA ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5∘ and the prism is made of a material of refractive index 1.5, the angle of incidence is
View SolutionA ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5∘ and the prism is made of a material of refractive index 1.5, the angle of incidence is.
View SolutionA ray of monochormatic light is incident on one refracting face of a prism of angle 75∘. It passes through the prism an is incident on the other at the critical angle. If the refractive index of the material of the prism is √2, the angle of the first face of the prism is
View SolutionA monochromatic light is incident on a glass prism of angle A. If the refractive index of a prism material mu If, a beam incident at an angle on the face AB will be transmitted through the AC of the prism, for which the correct option is:
View SolutionA ray of monochromatic light is incident on one refracting face of a prism of angle 75∘. It passes through the prism and is incident on the other face at the critical angle. If the refractive index of the material of the prism is √2 , the angle of incidence on the first face of the prism is,
View SolutionA ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5∘ and the prism is made of a material of refractive index 1.5, the angle of incidence is.
View Solution

