The design of some physical instrument requires that there be a constant difference in length of 10 cm between an iron rod and a copper cylinder laid side by side at all temperature find their lengths
(αFe=11×106.∘C−1,αCu=17×10−6.∘C−1)
28.3 cm, and 18.3 cm
23.8 cm, 13.8 cm
28.9 cm, 10.9
27.5 cm, 14.5 cm
The correct Answer is:A
To solve the problem of maintaining a constant length difference of 10 cm between an iron rod and a copper cylinder at all temperatures, we will follow these steps:
Step 1: Understand the relationship between lengths and temperature
The change in length of a rod due to temperature change is given by the formula:
ΔL=L0⋅α⋅ΔT
where:
- ΔL is the change in length,
- L0 is the original length,
- α is the coefficient of linear expansion,
- ΔT is the change in temperature.
Step 2: Set up the initial condition
Let:
- LFe = length of the iron rod,
- LCu = length of the copper cylinder.
According to the problem, the initial condition is:
LFe−LCu=10 cm
Step 3: Express the change in lengths
The change in lengths for both materials when the temperature changes can be expressed as:
ΔLFe=LFe⋅αFe⋅ΔT
ΔLCu=LCu⋅αCu⋅ΔT
Step 4: Set up the equation for constant length difference
For the length difference to remain constant at 10 cm, the change in length of the iron rod must equal the change in length of the copper cylinder:
ΔLFe−ΔLCu=0
This implies:
LFe⋅αFe⋅ΔT=LCu⋅αCu⋅ΔT
Since ΔT is common and non-zero, we can cancel it out:
LFe⋅αFe=LCu⋅αCu
Step 5: Relate the lengths of the rods
From the above equation, we can express the lengths in terms of each other:
LFeLCu=αCuαFe
Substituting the values of the coefficients of linear expansion:
αFe=11×10−6∘C−1,αCu=17×10−6∘C−1
Thus:
LFeLCu=17×10−611×10−6=1711
This implies:
LFe=1711LCu
Step 6: Substitute into the initial condition
Now substitute LFe into the initial condition:
1711LCu−LCu=10
This simplifies to:
17LCu−11LCu11=10
6LCu11=10
Step 7: Solve for LCu
Multiplying both sides by 11:
6LCu=110
Dividing by 6:
LCu=1106≈18.33 cm
Step 8: Find LFe
Now substitute LCu back to find LFe:
LFe=1711⋅18.33≈28.33 cm
Final Answer
Thus, the lengths are:
- Length of the iron rod LFe≈28.33 cm
- Length of the copper cylinder LCu≈18.33 cm
The change in length of a rod due to temperature change is given by the formula:
ΔL=L0⋅α⋅ΔT
where:
- ΔL is the change in length,
- L0 is the original length,
- α is the coefficient of linear expansion,
- ΔT is the change in temperature.
Let:
- LFe = length of the iron rod,
- LCu = length of the copper cylinder.
LFe−LCu=10 cm
The change in lengths for both materials when the temperature changes can be expressed as:
ΔLFe=LFe⋅αFe⋅ΔT
ΔLCu=LCu⋅αCu⋅ΔT
For the length difference to remain constant at 10 cm, the change in length of the iron rod must equal the change in length of the copper cylinder:
ΔLFe−ΔLCu=0
This implies:
LFe⋅αFe⋅ΔT=LCu⋅αCu⋅ΔT
Since ΔT is common and non-zero, we can cancel it out:
LFe⋅αFe=LCu⋅αCu
From the above equation, we can express the lengths in terms of each other:
LFeLCu=αCuαFe
Substituting the values of the coefficients of linear expansion:
αFe=11×10−6∘C−1,αCu=17×10−6∘C−1
Thus:
LFeLCu=17×10−611×10−6=1711
This implies:
LFe=1711LCu
Now substitute LFe into the initial condition:
1711LCu−LCu=10
This simplifies to:
17LCu−11LCu11=10
6LCu11=10
Multiplying both sides by 11:
6LCu=110
Dividing by 6:
LCu=1106≈18.33 cm
Now substitute LCu back to find LFe:
LFe=1711⋅18.33≈28.33 cm
Thus, the lengths are:
- Length of the iron rod LFe≈28.33 cm
- Length of the copper cylinder LCu≈18.33 cm
টপার এই প্রশ্নগুলো সমাধান করেছে
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Multiple Correct
25 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Comprehension
30 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Subjective
25 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Video
সম্পর্কিত প্রশ্ন
Due to thermal expansion with rise in temperature:
View SolutionA body cools in a surrounding of constant temperature 30∘C Its heat capacity is 2J/∘C. Initial temperature of cooling is valid. The body of mass 1 kg cools to 38∘C in 10 min
When the body temperature has reached 38∘C, it is heated again so that it reaches 40∘C in 10 min. The heat required from a heater by the body is
View SolutionA lead ball at 25∘C is dropped from a height of 2 km. It is heated due to air resistance and it is assumed that all of its kinetic energy is used in increasing the temperature of ball. Find the final temperature of the ball.
View SolutionThe displacement of a particle is given by y=(6t2+3t+4)m, where t is in seconds. Calculate the instantaneous speed of the particle.
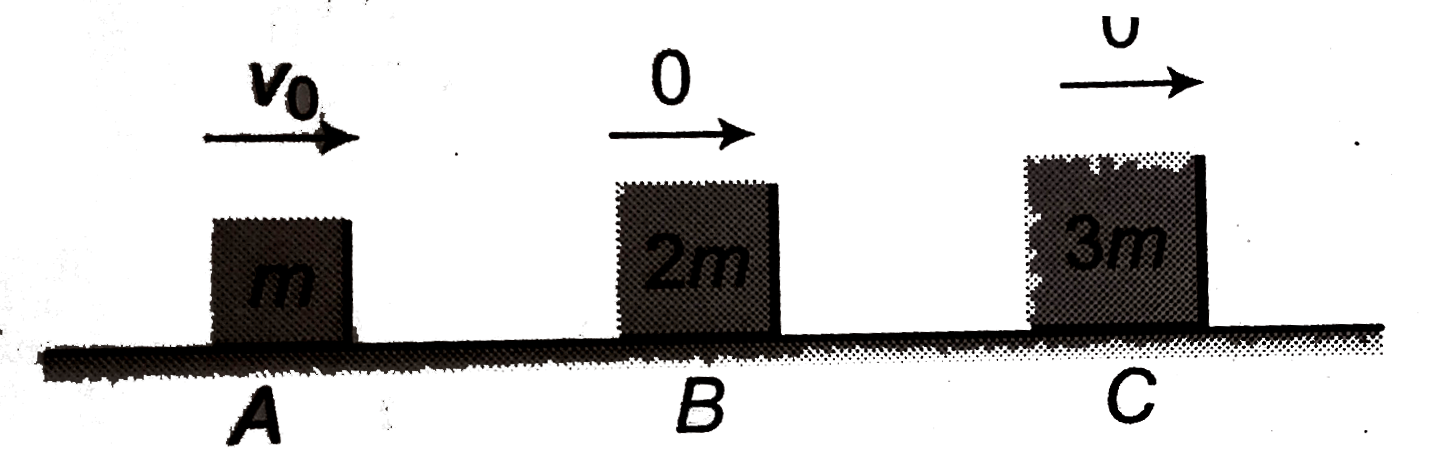
View SolutionThree objects A ,B and C are kept in a straight line on a smooth horizontal surface. These have masses m, 2m and 3m , respectively . The head - on elastic collision takes place between A and B and then B makes completely inelastic collision with C. All motions occur on the same straight line. The final speed of C will be
View SolutionThe design of some physical instrument requires that there be a constant difference in length of 10 cm between an iron rod and a copper cylinder laid side by side at all temperature find their lengths
(αFe=11×106.∘C−1,αCu=17×10−6.∘C−1)
View SolutionWhat should be the length of steel and copper rods at 0^(@)C that the length of steel rod is 5 cm longer than copper at all termperature? Given alpha_(Cu) = 1.7 xx 10^(5) .^(@)C^(-1) and alpha_(steel) = 1.1 xx 10^(5) .^(@)C^(-1) .
View Solution20∘C ताप पर एक स्टील पैमाना, ताँबे के एक तार की लम्बाई 80 सेमी नापता है। 40∘C ताप पर वही पैमाना उस तार को लम्बाई नापेगा (α steel =11×10−6∘C,α copper=17×10−6∘C−1 ) :
View SolutionThe length of the steel rod which would have the same difference in length with a copper rod of length 24cm at all temperatures. (alpha_("copper") = 18 xx 10^(-6) K^(-1) alpha_("steel") = 12 xx 10^(-6) k^(-1)) is -
View SolutionThe difference in length of an iron rod and a copper rod at 50^(@)C is 2 cm. This difference remains the same also at 450^(@)C . What are the lengths of the rods at 0^(@)C ? Given, alpha for iron =12 times 10^(-6@)C^(-1) and alpha for copper =17 times 10^(-6@)C^(-1) .
View SolutionThe difference in lengths of an iron and a copper rod, both at 50^(@)C " and " 450^(@)C , is 2 cm. What are the lengths of the two rods at 0^(@)C ? [Given, alpha_(Fe)=12 times 10^(-6@)C^(-1) " and " alpha_(Cu)=17 times 10^(-6@)C^(-1) ]
View SolutionThe length of a brass rod at 20^@C is observed to be 0.8 m when measured by an iron scale, correct at 0^@C . What will be the correct length of the rod at 0^@C ? Take, alpha_("iron") = 1.2 xx 10^(-5) ""^@C^(-1) alpha_("brass") = 1.9 xx 10^(-5) ""^@C^(-1)
View SolutionIn a certain arrangement, two cylinders of brass and steel are laid side by side and there is a constant difference of length between them at any temperature. Calculate the lengths of these cylinders at 0∘C if there is a difference of 5 cm between their lengths at all temperatures.
αbrass=0.0000019∘C−1
αsteel=1.2×10−6C−1
View SolutionIt is found in the shape of an instrument that the lengths of cylindrical sticks of iron and copper are found on all the thermos. 10 cm Has a fixed end. If a_(Fe) = 11 xx 10^(-6^(@)C^(-1) And alpha_(Cu) = 17 xx 10^(-6).^(@)C^(-1) If we find their lengths respectively?
View SolutionBy a steel scale, the length of a copper wire is measured to be 80.0 cm. 20^(@) C is the temperature (which is the calibration temperature of the scale) 40^(@) C will be the length of the wire measured by the scale at the temperature ( alpha_(इस्ताप) = 11 xx 10^(-6) per^(@) C And alpha_(तांबा) = 17 xx 10^(-6)"per "^(@)C )
View SolutionIf the steel rod is 5 cm taller than the copper rod at any temperature, 0^@C What should be the length of steel and copper rods on heating? alpha_("steel") = 1.1 xx 10^(-5) ""^@C^(-1) alpha_("coper") = 1.7 xx 10^(-5) ""^@C
View Solution

