The system shown in fig, is released from rest. Calculate the tension in the string and the force exerted by the string on the pulleys, assuming pulleys and strings are massless.

The correct Answer is:mgsinθM+2m(1−cosθ).
Let acceleration of the wedge be a leftwards then acceleration of block, relative to the wedge will also be equal to a but down the incline. Hence, net acceleration of the block will be equal to vector sum of these two as shown in fig.
Now considering FBD's

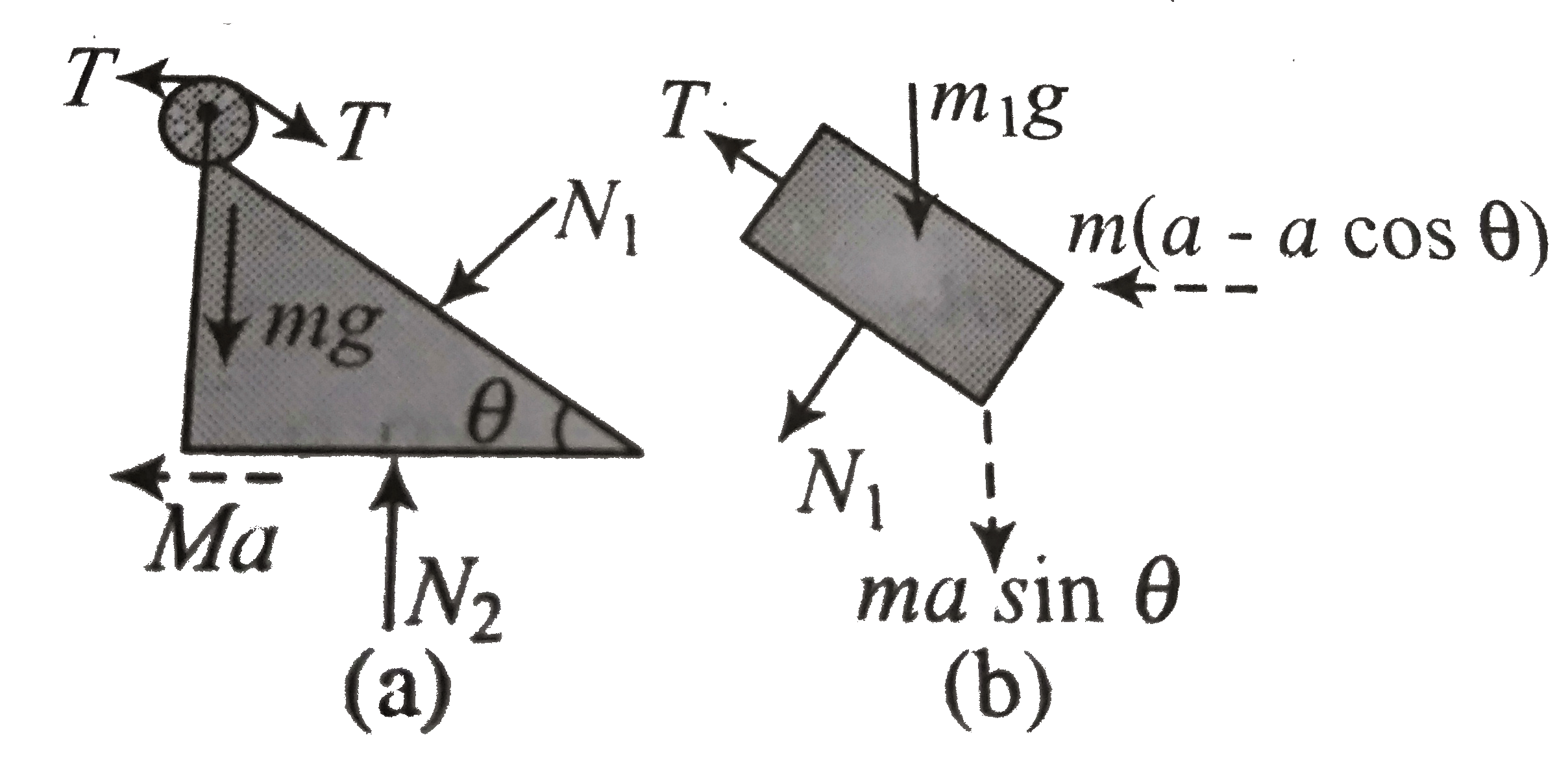
For the wedge,
N2=Tsinθ+N1cosθ..(i)
T−Tcosθ+N1sinθ=Ma ..(ii)
For the block,
mg−N1cosθ=masinθ ..(iii)
Tcosθ−N1sinθ=m(a−acosθ)
Solving above equation, a=mgsinθM+2m(1−cosθ).
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Single Correct
Explore 73 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Multiple Correct
Explore 11 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Exercise 6.4
Explore 13 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
Two skaters have weight in the ratio 4:5 and are 9m apart, on a smooth frictionless surface. They pull on a rope stretched between them. The ratio of the distance covered by them when they meet each other will be
View SolutionA block of mass m=10kg is suspended with the help of three strings as shown in fig. Find the tensions T1 and T2.

View Solution(a) A 10-kg block is supported by cord that runs to a spring scale, which is supported by another cord from the ceiling as shown in fig. What is the reading on the scale?

(b) In Fig. the block is supported by a cord that runs around a pulley and to a scale. The opposite end of the scale is attached by a cord to a wall. What is the reading of the scale?

(c ) In fig. the wall has been replaced with a second 10-kg block, what is the reading on the scale now?
 .
.
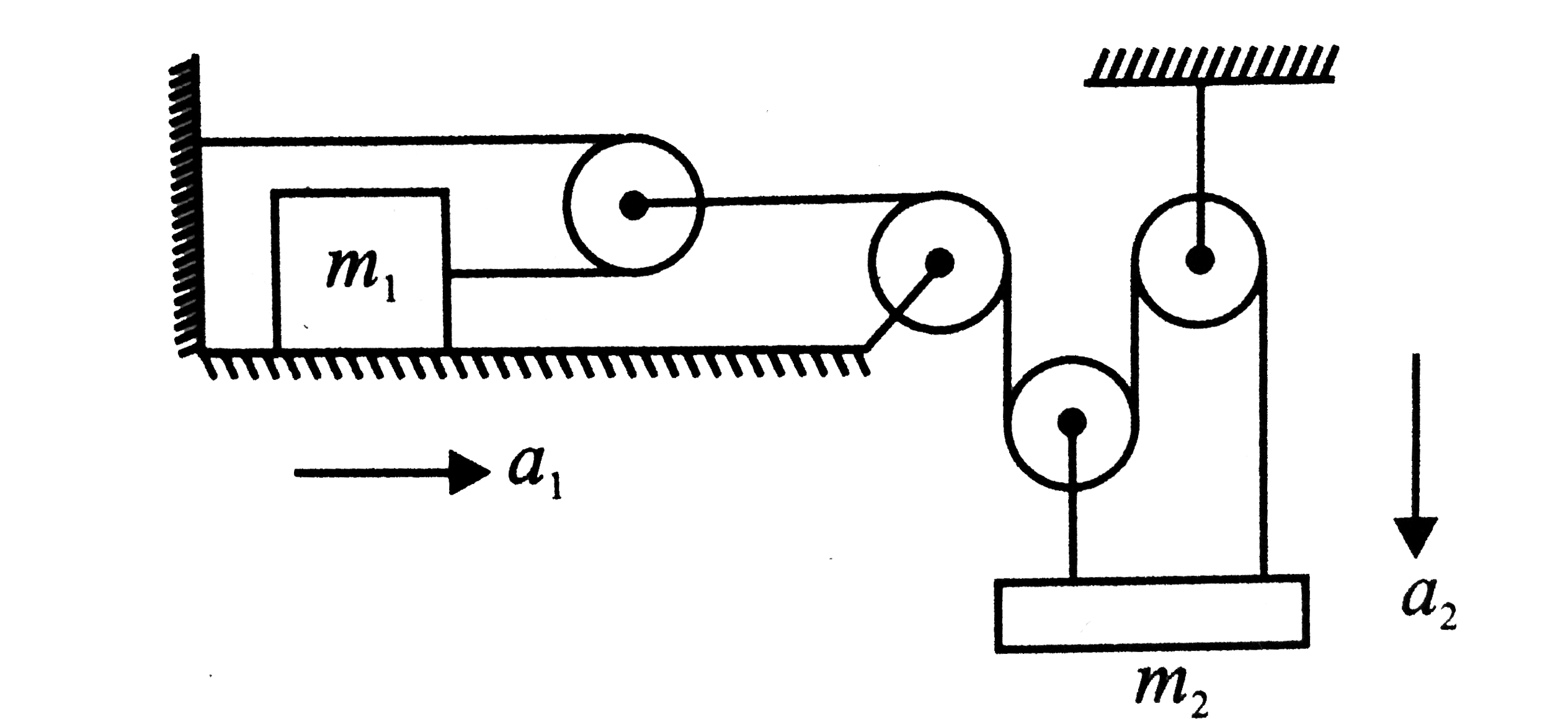
View SolutionTwo blocks are arranged as shown in figure. Find the ratio of a1/a2. (a1 is acceleration of m1 and a2 that of m2)
View SolutionA block is moving on an inclined plane making an angle 45∘ with the horizontal and the coefficient of friction is μ. The force required to just push it up the inclined plane is 3 times the force required to just prevent it from sliding down. If we define N=10μ, then N is
View SolutionThe system shown in fig, is released from rest. Calculate the tension in the string and the force exerted by the string on the pulleys, assuming pulleys and strings are massless.

View SolutionFind the acceleration blocks in fig. The pulley and the string are massless.

View SolutionIn the shown mass pulley system, pulleys and string are massless. The one end of the string is pulleed by the force F=2mg . The acceleration of the block will be
View SolutionThe tension in the string in the pulley system shown in .
View SolutionFind the acceleration and tension in the string in the following cases . The pulley and string are massless. (a) (b)
View SolutionThe pulley is light and smooth : the strings are inextensible and light. The system is released from rest, find the acceleration of each block, tensions in the strings and reaction in pulley.
View SolutionIn the shown mass pulley system, pulleys and string are massless. The one end of the string is pulled by the force F = mg. The acceleration of the block will be :

View SolutionIn the system shown in fig the pulley is frictionless and the string massless if m_(1)=m_(2) thrust on the pulley will be:
View SolutionThe system shown in th fig is released from rest. (Neglecting friction and mass of the pulley, string and spring). The spring can be elongated:
View SolutionAssume that all the pulleys are massless and frictionless and strings to be inextensible.
View SolutionMass of the pulley is m & radius is R. Assume pulley to be disc. Block of mass m is released from the position shown. String is massless & inextensible. There is no slipping between rope and pulley. The impulse exerted by the string on the pulley at the moment string becomes taut is J then (2msqrt(gR))/(J) is equal to
View Solution
