The value of (Cp−Cv) is 1.00R for a gas sample in state A and is 1.08 R in state B. Let (pA,pB)denote the pressures and (TAandTB) denote the temperatures of the states A and B respectively . Most likely
pA<pB and TA>TB
pA>pBandTA<TB
pA=pBandTA<TB
pA>pBandTA=TB
The correct Answer is:A
Step by step video, text & image solution for The value of (C_p - C_v) is 1.00 R for a gas sample in state A and is 1.08 R in state B. Let (p_A, p_B)denote the pressures and (T_A and T_B) denote the temperatures of the states A and B respectively . Most likely by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SPECIFIC HEAT CAPACITIES OF GASESBOOK - HC VERMACHAPTER - SPECIFIC HEAT CAPACITIES OF GASESEXERCISE - Objective 2
7 Videos
- SPECIFIC HEAT CAPACITIES OF GASESBOOK - HC VERMACHAPTER - SPECIFIC HEAT CAPACITIES OF GASESEXERCISE - Exercises
35 Videos
- SPECIFIC HEAT CAPACITIES OF GASESBOOK - HC VERMACHAPTER - SPECIFIC HEAT CAPACITIES OF GASESEXERCISE - Short Answer
10 Videos
- SOUND WAVESBOOK - HC VERMACHAPTER - SOUND WAVESEXERCISE - Exercises
89 Videos
- THE FORCESBOOK - HC VERMACHAPTER - THE FORCESEXERCISE - Exercises
12 Videos
Similar Questions
A gas kept in a container of finite conductivity is suddenly compressed . The process
View SolutionA vessel containing one of mole of a monatomic ideal gas (mo≤ca––rweight=20gmol^(1)) is moving on a floor at a speed of 50ms−1 The vessel is stopped suddenly. Assuming that the mechanical energy lost has gone into the internal energy of the gas , find the rise in its temperature .
View SolutionDoes a gas have just two specific heat capacities or more than two ? Is the number of specific heat capacicties of a gas countable?
View SolutionA steel tube of length 1.00 m is struck at one end. A person with his er close to the othr end hears the sound of the blow twice one travelign through the body of the tube and the other through the air in the tube. Find the time gap between the two hearings. Use the table in the next for speeds of sound in various substances.
View SolutionThe gravitational force acting on a particle of 1 g due to a similar particle is equal to 6.67×10−17N. Calculate the separation between the particles.
View SolutionTwo samples A and B are initaially kept in the same state. The sample A is expanded through an adiabatic process and the sample B through an isothermal process. The final volumes of the samples are the same . The final pressures in A and B are p_A and P_B respectively.
View SolutionLet TaandTb be the final temperatures of the samples A and B respectively in the previous question.
View Solution1.0 k-mol of a sample of helium gas is put through the cycle of operations shown in figure. BC is an isothermal process and p_A=1.00 atm , V_A=22.4m^3 , p_B=2.00atm . What are T_A , T_B and V_C ?
View SolutionThe value of CP−Cv=1.00R for a gas in state A and CP−Cv=1.06R in another state. If PA and PB denote the pressure and TA and TB denote the temperature in the two states, then
View SolutionThe value of Cp−Cv is 1.09R for a gas sample in state A and is 1.00R in state B. Let AA,TB denote the temperature and pA and PB denote the pressure of the states A and B respectively. Then
View SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A to B adiabatic expansion B to C: cooling at constant volume C to D adiabatic compression D to C: heating at constant volume. The pressure and temperature at P_A, P_B etc. T_A , T_B etc. are denoted etc. respectively. Given that T_A = 1000 K, P_B =(2 //3)P_A and P_C = (1 //3)P_A Calculate the following quantities. The work done by the gas in process A to B (in J)
View SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion
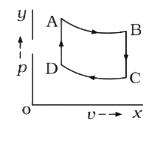
B→C: cooling at constant volume
C→D adiabatic compression D→C: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(t/3)PA
Calculate the following quantities.
The heat lost by the gas in process B→C (in J)
View SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion
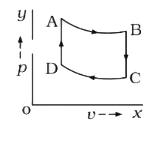
B→C: cooling at constant volume
C→D adiabatic compression D→A: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(1/3)PA
Calculate the following quantities.
The temperature TD (in K) [Given : (25)2/5=0.85 ]
View SolutionThe molar specific heats of an ideal gas at constant pressure and volume arc denoted by CP and CV respectively. If γ=CPCVandR is the universal gas constant, then CV is equal to
View SolutionThe value of CP−Cv=1.00R for a gas in state A and CP−Cv=1.06R in another state. If PA and PB denote the pressure and TA and TB denote the temperature in the two states, then
View Solution

