Two block A and B of masses 1kg and2kg respectively are connected by a string, passing over a light frictionless pulley B as shown. Another string connect the center of pulley. Both the blocks are resting on a horizontal floor and the pulley is help such that string remains just taut. At moment t=0, a force F=20t starts acting on the pully along vertically upwards direction as shown in figure.Calculate

(a) velocity of A when B loses contact with the floor.
(b) height raised by the pulley upto that instant.
(Take =g=10m/s2)
A loses contact at t=2s.
C loses contact at t=1.5s.
A and B lose contact at the same time.
All three blocks lose contact at the same time.
The correct Answer is:B
T3=20t,T1=T2=10t
For A to lose contact: 10t=1g⇒1s
For B to lose contact: 10t=2g⇒2s
For C to lose contact: 20t=3g⇒1.5s
aA=T1−1g1 velocity of A when B loses contact.
V1=∫21aAdt=∫21(10t−g)dt=5ms−1
At t=2s,aB=0,aA=10×2×−101=10ms−2
aA/B=aA−aB=10−0=10ms−2.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Assertion-reasoning
Explore 15 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
A block is placed on an inclined plane moving towards right horizontally with an acceleration a0=g. The length of the plane AC=1m. Friction is absent everywhere. Find the time taken (in seconds) by the block to reach from C to A.
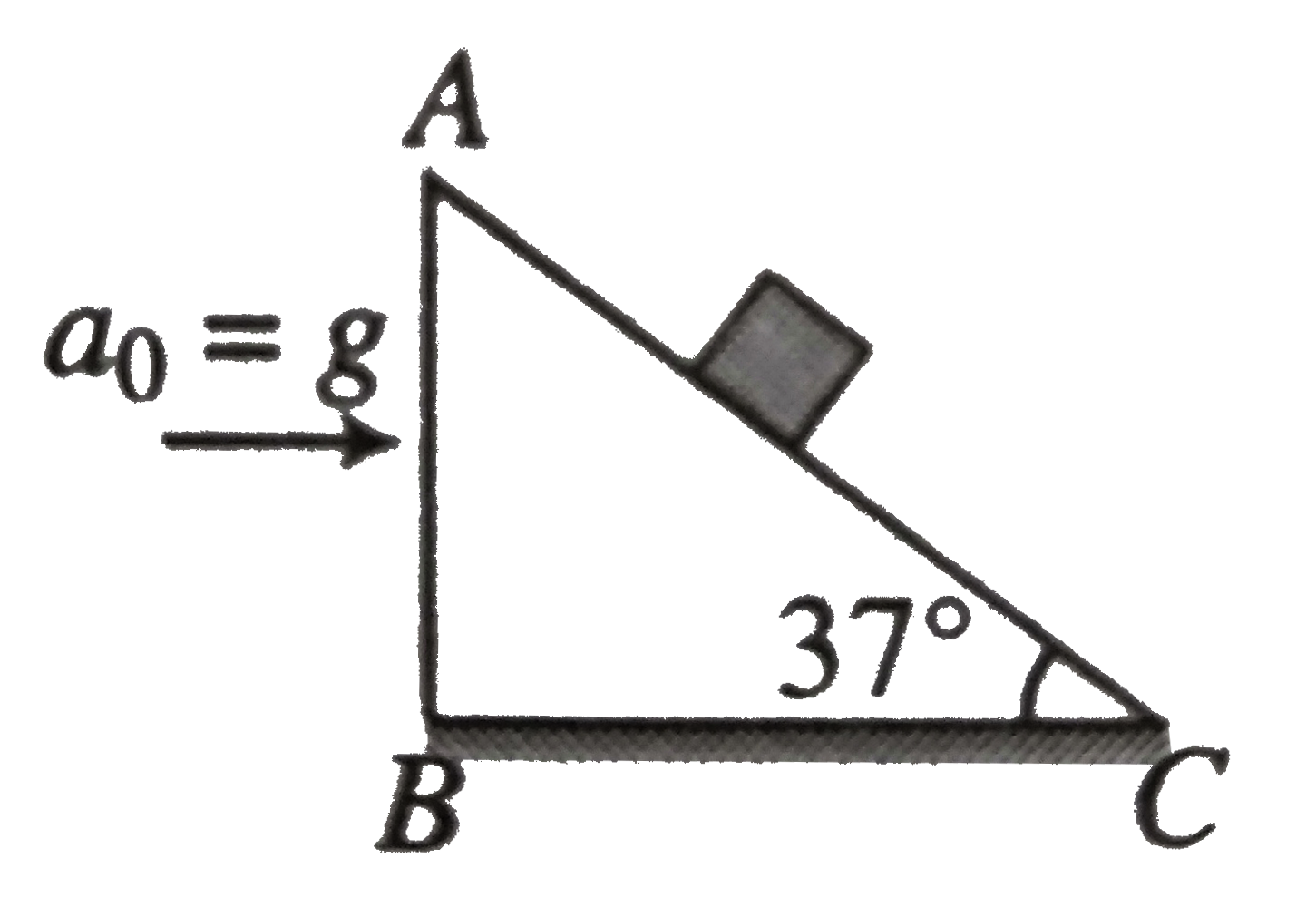
View SolutionStatement I: The driver of a moving car sees a wall in front of him. To avoid collision, he should apply brakes rather than taking a turn away from the wall.
Statement II: Frictional force is needed to stop the car or taking a turn on a horizontal road.
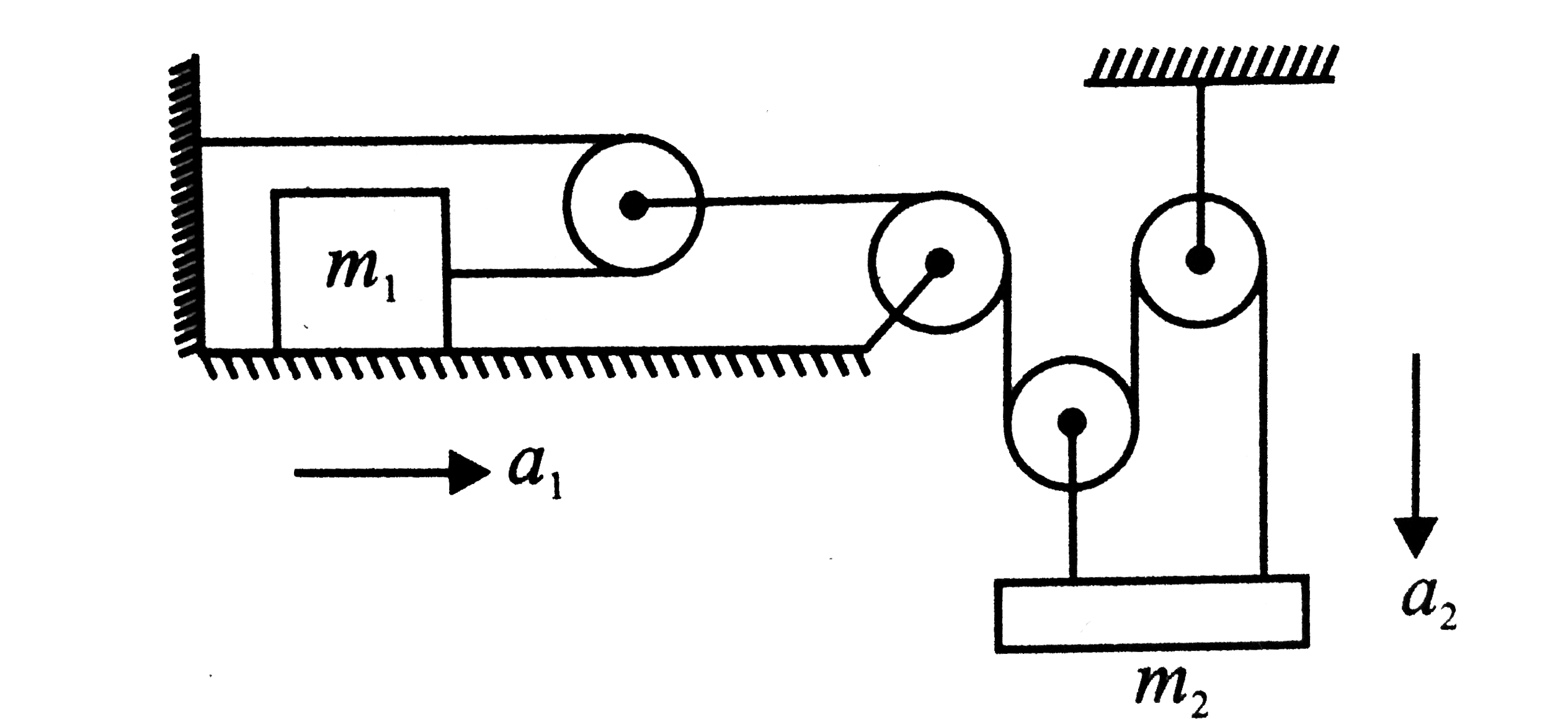
View SolutionTwo blocks are arranged as shown in figure. Find the ratio of a1/a2. (a1 is acceleration of m1 and a2 that of m2)
View SolutionA block is moving on an inclined plane making an angle 45∘ with the horizontal and the coefficient of friction is μ. The force required to just push it up the inclined plane is 3 times the force required to just prevent it from sliding down. If we define N=10μ, then N is
View SolutionTwo block of masses m =5kg and M =10kg are connected by a string passing over a pulley B as shown. Another string connect the center of pulley B to the floor and passes over another pulley A as shown. An upwards force F is applied at the center of pulley A . Both the pulleys are massless. Find the acceleration of block m and M , if F is (a) 100N 300N 500N(Take g = 10m//s^(2))
View SolutionTwo block A and B of masses 1kg and2kg respectively are connected by a string, passing over a light frictionless pulley B as shown. Another string connect the center of pulley. Both the blocks are resting on a horizontal floor and the pulley is help such that string remains just taut. At moment t=0, a force F=20t starts acting on the pully along vertically upwards direction as shown in figure.Calculate

(a) velicity of A when B loses contact with the floor.
(b) height raised by the pulley upto that instant.
(Take =g=10m/s2)
View SolutionTwo blocks A and B , each of mass 10 kg , are connected by a light string passing over a smooth pulley as shown in the figure. Block A will remain at rest if the friction on it is
View SolutionTwo blocks are connected by an inextensible light string, the string is passing over smooth, light pulley as shown. Find the acceleration of blocks and tension in the string, reaction in pulley.
View SolutionTwo block of A and B of mass 1kg and 2kg are hung from light pulley. Initially the block B is held stationary. At t=0 block B is given velocity 10m//s in upward direction. String and pulley are light and there is no friction anywhere. Total mechanical energy lost when the string becomes taut is
View SolutionTwo blocks are connected by a string that passes over a pulley of radius R and moment of inertia I. The block of mass m1 sides on a frictionless, horizontal surface, the block of mass m2 is suspended from the string. Find the acceleration a of the blocks and the tension T1 and T2 assuming that the string does not slip on the pulley.

View SolutionThere blocks a,b and c of massses 10 kg ,10 kg and 20 kg respectivaly are arrenged as shown in figure all the surface are frictionless and string is inextensible A constant force F= 20N MN is applied on block a as shown .pulley and string are light . part of block a as shown . pulley and string are light . part of the string connecting both pulleys is vertical and part of hte stings connecting pulleys with masses a and b are horizontal .
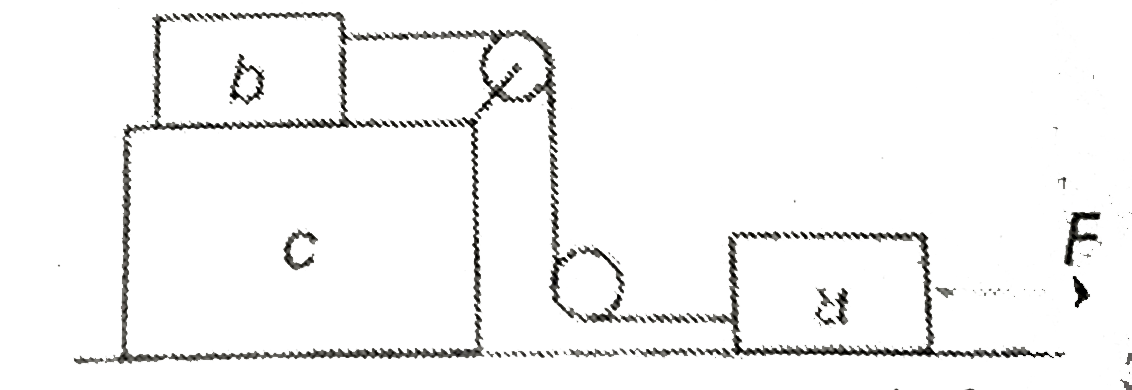
View SolutionTwo blocks A and B having masses m1=1kgm2=4kg are arranged as shown in the figure The pulleys P and Q are light and frictionless. All the blocks are resting on a horizontal floor and the pulleys are held such that strings remains just taut. At moment t=0 a force F=30 t (N) starts acting on the pulley P along vertically upward direction as shown in the figure The time when the blocks A and B loose contact with ground is 4/x sec then x is:
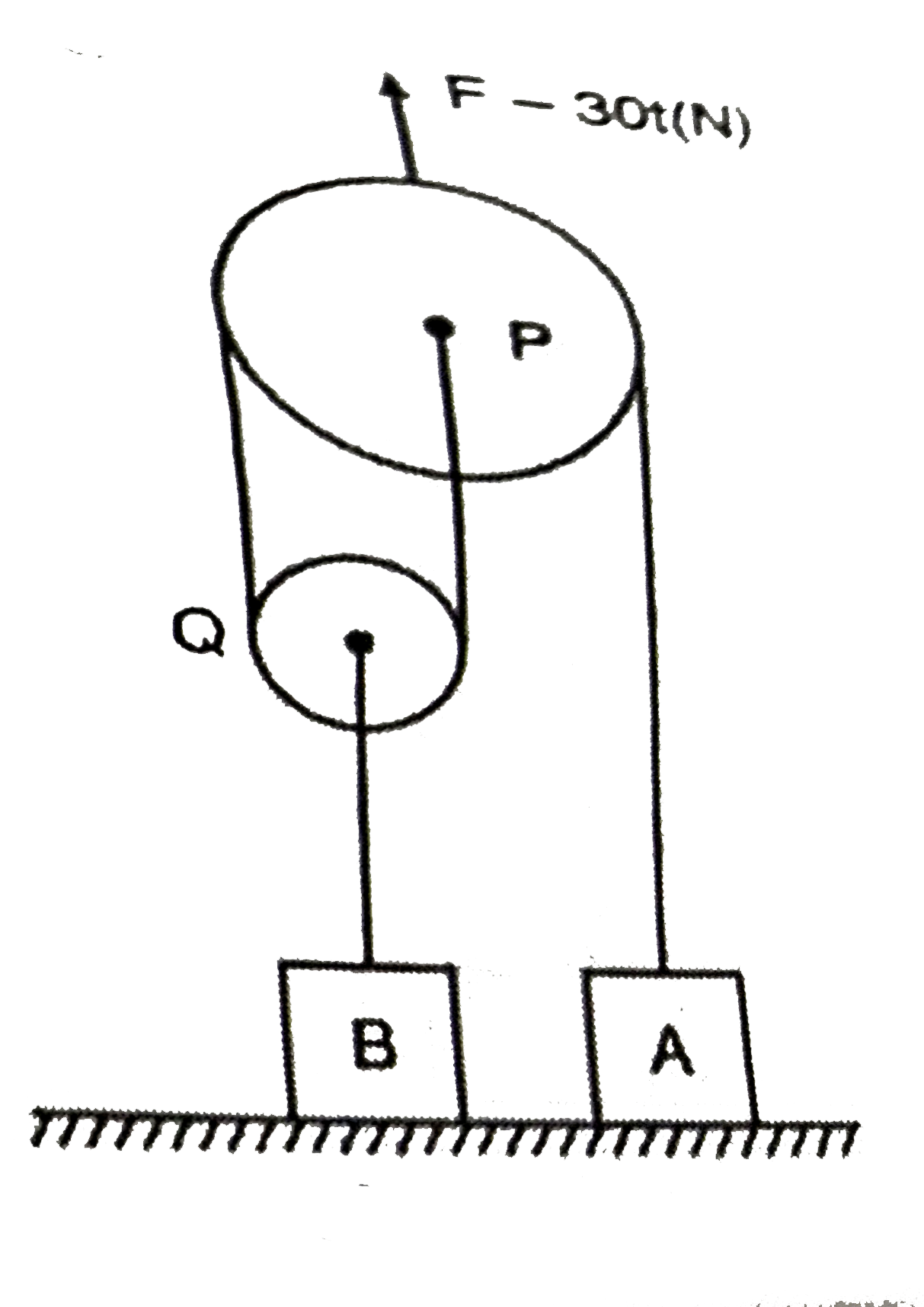
View SolutionTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
View SolutionTwo blcoks of mass 10kg and 2kg respectively are connected by an ideal string passing over a fixed smooth pulley as shown in figure. A monkey of 8kg started climbing the string with constant accleration 2ms^(-2) with respect to string t=0. Initially the monkey is 2.4m from the pulley. Find the time taken by the monkey to reach the pulley.
View SolutionTwo blocks each of mass m are connected over two light and frictionless pulleys and a fixed wedge by a light string as shown in figure. The tension in the string is :
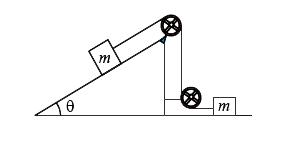
View SolutionString going over a pulley connects two blocks of masses m, and my. String and pulley are light. Calculate acceleration of centre of mass of blocks system.

View Solution
