Which of the following pairs has the same dimensions?
Torque and work
Angular momentum and Planck's constant
Energy momentum and Planck's constant
Light year and wavelength
The correct Answer is:A, B, D
To determine which of the given pairs has the same dimensions, we will analyze each pair one by one.
Step 1: Analyze Torque and Work
- Torque (τ) is defined as the product of force (F) and the distance (r) from the pivot point. The formula is:
τ=F⋅r
The dimension of force (F) is given by:
F=m⋅a=m⋅LT2⟹(F)=MLT−2
Therefore, the dimension of torque is:
(τ)=(F)⋅(r)=(MLT−2)⋅L=ML2T−2
- Work (W) is also defined as the product of force and displacement:
W=F⋅d
Thus, the dimension of work is:
(W)=(F)⋅(d)=(MLT−2)⋅L=ML2T−2
Since both torque and work have the same dimensions:
(τ)=(W)=ML2T−2
Step 2: Analyze Angular Momentum and Planck Constant
- Angular Momentum (L) is defined as:
L=r⋅p=r⋅(m⋅v)=r⋅(m⋅LT)
Thus, the dimension of angular momentum is:
(L)=(r)⋅(p)=L⋅(MLT−1)=ML2T−1
- Planck Constant (h) has the dimension:
(h)=E⋅T=(ML2T−2)⋅T=ML2T−1
Since both angular momentum and Planck constant have the same dimensions:
(L)=(h)=ML2T−1
Step 3: Analyze Energy Momentum and Planck Constant
- Energy (E) has the dimension:
(E)=ML2T−2
- Momentum (p) has the dimension:
(p)=m⋅v=M⋅LT=MLT−1
Since energy and momentum do not have the same dimensions, this pair is not valid.
Step 4: Analyze Light Year and Wavelength
- Light Year is a measure of distance, hence:
(Light Year)=L
- Wavelength is also a measure of distance, hence:
(Wavelength)=L
Since both light year and wavelength have the same dimensions:
(Light Year)=(Wavelength)=L
Conclusion
The pairs that have the same dimensions are:
1. Torque and Work
2. Angular Momentum and Planck Constant
3. Light Year and Wavelength
Summary of Pairs with Same Dimensions:
- Torque and Work: ML2T−2
- Angular Momentum and Planck Constant: ML2T−1
- Light Year and Wavelength: L
- Torque (τ) is defined as the product of force (F) and the distance (r) from the pivot point. The formula is:
τ=F⋅r
The dimension of force (F) is given by:
F=m⋅a=m⋅LT2⟹(F)=MLT−2
Therefore, the dimension of torque is:
(τ)=(F)⋅(r)=(MLT−2)⋅L=ML2T−2
W=F⋅d
Thus, the dimension of work is:
(W)=(F)⋅(d)=(MLT−2)⋅L=ML2T−2
(τ)=(W)=ML2T−2
- Angular Momentum (L) is defined as:
L=r⋅p=r⋅(m⋅v)=r⋅(m⋅LT)
Thus, the dimension of angular momentum is:
(L)=(r)⋅(p)=L⋅(MLT−1)=ML2T−1
(h)=E⋅T=(ML2T−2)⋅T=ML2T−1
(L)=(h)=ML2T−1
- Energy (E) has the dimension:
(E)=ML2T−2
(p)=m⋅v=M⋅LT=MLT−1
- Light Year is a measure of distance, hence:
(Light Year)=L
(Wavelength)=L
(Light Year)=(Wavelength)=L
The pairs that have the same dimensions are:
1. Torque and Work
2. Angular Momentum and Planck Constant
3. Light Year and Wavelength
- Torque and Work: ML2T−2
- Angular Momentum and Planck Constant: ML2T−1
- Light Year and Wavelength: L
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Multiple Correct
Explore 2 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Linked Comprehension
Explore 3 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Subjective
Explore 31 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
Dimensionsal methods provide three major advantages in verification , deviation , and changing the system of units . Any empirical formula that is derived based on this method has to be verified and propportionality constants found by experimental means . The presence or absence of certain factors - non dimensional constants or variables - cannot be identified by this method . So every dimensionally correct relation cannot be taken as perfectly correct.
The time period of oscillation of a drop depends on surface tension σ , density of the liquid ρ , and radius r . The relation is
View SolutionThe accuracy of measurement also lies in the way the results is expressed. The number of digits to which a value is to be expressed is one digit more than number of digits after after an operation is carried out on the given values. The error can be minimised by many trials and using the correct methods are instruments.
If the length and breadth are measured as 4.234and1.05m, the area of the rectangle is
View Solutionαt2=Fv+βx2
Find the dimension formula for [α]and[β] ( here t = time , F = force , v = velocity , x = distance).
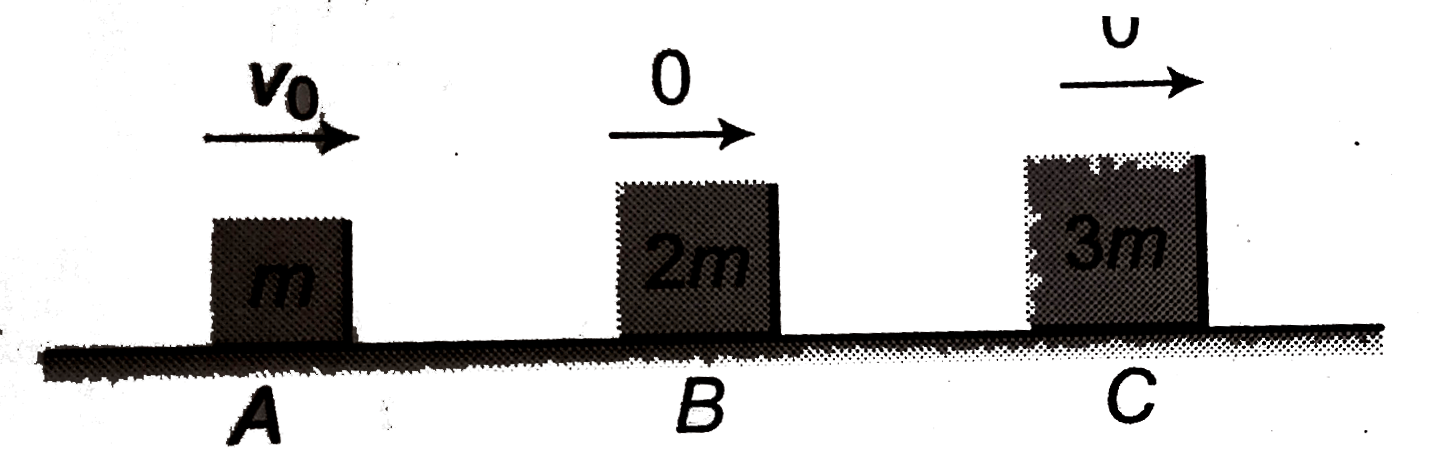
View SolutionThree objects A ,B and C are kept in a straight line on a smooth horizontal surface. These have masses m, 2m and 3m , respectively . The head - on elastic collision takes place between A and B and then B makes completely inelastic collision with C. All motions occur on the same straight line. The final speed of C will be
View SolutionA cyclindrical vessel of height 500 mm has an orifice (small hole) at its bottom. The orifice is initially closed any water is filled in ti upto height H.Now the top is completely sealed with a cap and the orifice at the bottom is opened .Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. The fall in height (in mm) of water level due to opening of the orifice is [ Take atmospheric pressure = 1.0×105Nm2, density of water = 1000kgm3. Neglect any effect of surface tension.]
View SolutionWhich of the following pairs has quantities of the same dimensions?
View SolutionWhich of the following pairs has the same dimensions?
View SolutionWhich pair has the same dimensions?
View SolutionWhich pair has the same dimensions
View SolutionWhich of the following pairs of physical quantities has the same dimensions
View SolutionWhich one of the following pair of quantities has same dimension ?
View Solutionनिम्न में किस युग्म की विमाए समान नहीं है ?
View SolutionWhich one of the following pairs has the same dimensions ?
View Solutionकिस युग्म की विमाएँ समान हैं -
View SolutionWhich one of the following pair of quantities has the same dimension?
View Solution
