A hyperbola having the transverse axis of length 2 sin θ is confocal with the ellipse 3x2+4y2=12. Then its equation is
x2cosec2θ−y2sec2θ=1
x2sec2θ−y2cosec2θ=1
x2sin2θ−y2cos2θ=1
x2sin2θ−y2cos2θ=1
The correct Answer is:A
Step by step video solution for A hyperbola having the transverse axis of length 2 sin theta is confocal with the ellipse 3x^(2)+4y^(2)=12. Then its equation is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HYPERBOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - HYPERBOLAEXERCISE - Hyperbola Exercise 11 : Questions Asked in Previous 13 Years Exams
3 Videos
- HYPERBOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - HYPERBOLAEXERCISE - Hyperbola Exercise 10 : Subjective Type Questions
3 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
10 Videos
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHS ENGLISHCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
Similar Questions
Matching the information given in the three columns of the following table column 1, 2 and 3 contain conics, equations of tangents in the conics and points of contact, respectively.
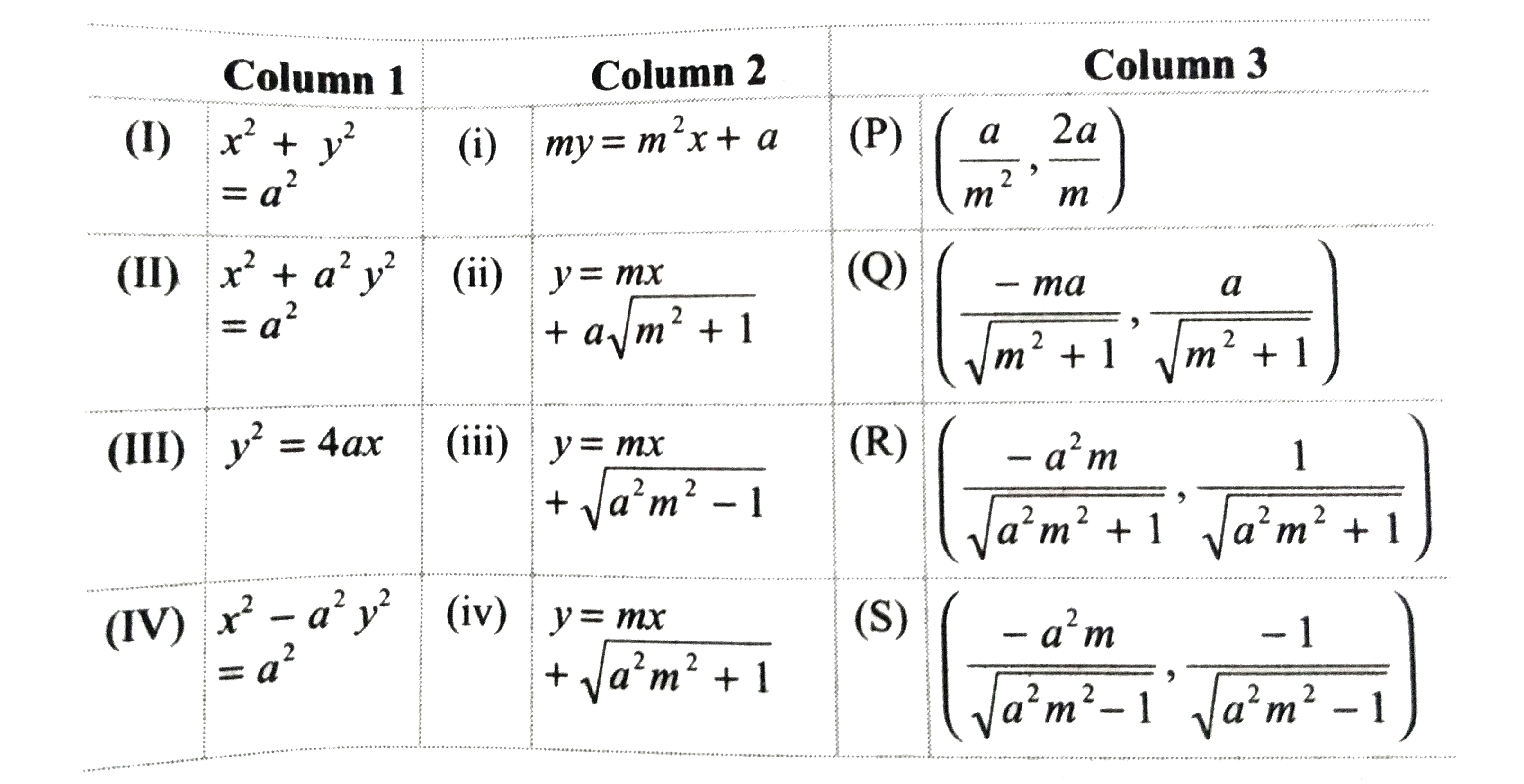
Q. The tangent to a suitable conic (column 1) at (√3,12) is found to be √3x+2y=4, then which of the following options is the correct combination?
View SolutionIf there are two points A and B on rectangular hyperbola xy=c2 such that abscissa of A =ordinate of B, then the locus of points of intersection of tangents at A and B is
View SolutionFind the number of solutions of the equation x21−|x−2|=1, graphically.
View SolutionThe integral ∫sec2x(secx+tanx)92dx equals (for some arbitrary constant K). −1(secx+tanx)112{111−17(secx+tanx)2}+K 1(secx+tanx)111{111−17(secx+tanx)2}+K −1(secx+tanx)112{111+17(secx+tanx)2}+K 1(secx+tanx)112{111+17(secx+tanx)2}+K
View SolutionA hyperbola,having the transverse axis of length 2sin theta, is confocal with the ellipse 3x^(2)+4y^(2)=12. Then its equation is
View SolutionA hyperbola having the transverse axis of length 12 unit is confocal with the ellipse 3x2+4y2=12, then
View Solutionएक अतिपरवलय जिसकी अनुप्रस्थ अक्ष की लम्बाई 2sinθ है तथा दीर्घवृत्त 3x2+4y2=12 की नाभियाँ सम्पाती हैं , तब अतिपरवलय की समीकरण है -
View Solutionएक अतिपरवलय जिसकी अनुप्रस्थ अक्ष की लम्बाई 2sinθ है, दीर्घवृत्त 3x2+4y2=12 के संनाभि (confocal) है | तब इसका समीकरण है
View SolutionA hyperbola, having the transverse axis of length 2 sinθ, is confocal with the ellipse 3x2+4y2=12. Then its equation is
View SolutionA hyperbola, having the transverse axis of length 2sinθ is confocal with the ellipse 3x2+4y2=12. Its equation is
View SolutionA hyperbola having the transverse axis of length √2 units has the same focii as that of ellipse 3x2+4y2=12, then its equation is
View Solutionएक अतिपरवलय, जिसकी अनुप्रस्थ अक्ष की लम्बाई 2sinθ है तथा दीर्घवृत 3x2+4y2=12 की नाभिया सम्पाती हैं। तब अतिपरवलय की समीकरण है
View SolutionA hyperbola having the transversal axis of length 2sinθ is confocal with the ellipse 3x2+4y2=12 Then its equations is :
View SolutionA hyperbola having the transverse axis of length 2 sin θ, is confocal with the ellipse 3x2+4y2=12. Then show that the equation of this hyperbola is x2sin2θ−y2cos2θ=1.
View SolutionA hyperbola, having the transverse axis of length 2sinθ, is confocal with the ellipse 3x2+4y2=12. Then its equation is
View SolutionA hyperbola having the transverse axis of length 12 unit is confocal with the ellipse 3x2+4y2=12, then
View Solution

