ABCD is a trapezium such that AB∣∣CDandCB is perpendicular to them. If ∠ADB=θ,BC=p,andCD=q , show that AB=(p2+q2)sinθpcosθ+qsinθ
To solve the problem, we need to show that in trapezium ABCD, with AB∥CD, CB⊥AB and AD making an angle θ with DB, the length of AB can be expressed as:
AB=(p2+q2)sinθpcosθ+qsinθ
where BC=p and CD=q.
1. Understanding the Geometry:
- Draw trapezium ABCD with AB∥CD and CB⊥AB.
- Label the points: A at the top left, B at the top right, C at the bottom right, and D at the bottom left.
2. Identifying Angles:
- Given ∠ADB=θ.
- Let ∠DBA=α. Since AB∥CD, ∠ABC=∠ADC=90∘.
3. Using the Sine Rule:
- In triangle ADB, apply the sine rule:
sinθAB=sin(π−α−θ)BD
- Since sin(π−x)=sinx, we can rewrite this as:
sinθAB=sin(α+θ)BD
4. Finding BD:
- Using the Pythagorean theorem in triangle BCD:
BD2=BC2+CD2=p2+q2
- Therefore, BD=√p2+q2.
5. Substituting BD:
- Substitute BD back into the sine rule equation:
AB=BD⋅sinθsin(α+θ)=√p2+q2⋅sinθsin(α+θ)
6. Finding sin(α+θ):
- Using the sine addition formula:
sin(α+θ)=sinαcosθ+cosαsinθ
7. Finding sinα and cosα:
- In triangle BCD:
- sinα=BCBD=p√p2+q2
- cosα=CDBD=q√p2+q2
8. Substituting sinα and cosα:
- Substitute these values into the sine addition formula:
sin(α+θ)=p√p2+q2cosθ+q√p2+q2sinθ
- Simplifying gives:
sin(α+θ)=pcosθ+qsinθ√p2+q2
9. Final Expression for AB:
- Substitute this back into the equation for AB:
AB=√p2+q2⋅sinθpcosθ+qsinθ√p2+q2
- This simplifies to:
AB=(p2+q2)sinθpcosθ+qsinθ
Conclusion:
Thus, we have shown that:
AB=(p2+q2)sinθpcosθ+qsinθ
- Draw trapezium ABCD with AB∥CD and CB⊥AB.
- Label the points: A at the top left, B at the top right, C at the bottom right, and D at the bottom left.
- Given ∠ADB=θ.
- Let ∠DBA=α. Since AB∥CD, ∠ABC=∠ADC=90∘.
- In triangle ADB, apply the sine rule:
sinθAB=sin(π−α−θ)BD
- Since sin(π−x)=sinx, we can rewrite this as:
sinθAB=sin(α+θ)BD
- Using the Pythagorean theorem in triangle BCD:
BD2=BC2+CD2=p2+q2
- Therefore, BD=√p2+q2.
- Substitute BD back into the sine rule equation:
AB=BD⋅sinθsin(α+θ)=√p2+q2⋅sinθsin(α+θ)
- Using the sine addition formula:
sin(α+θ)=sinαcosθ+cosαsinθ
- In triangle BCD:
- sinα=BCBD=p√p2+q2
- cosα=CDBD=q√p2+q2
- Substitute these values into the sine addition formula:
sin(α+θ)=p√p2+q2cosθ+q√p2+q2sinθ
- Simplifying gives:
sin(α+θ)=pcosθ+qsinθ√p2+q2
- Substitute this back into the equation for AB:
AB=√p2+q2⋅sinθpcosθ+qsinθ√p2+q2
- This simplifies to:
AB=(p2+q2)sinθpcosθ+qsinθ
Thus, we have shown that:
AB=(p2+q2)sinθpcosθ+qsinθ
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGE ENGLISHChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Concept application exercise 5.1
Explore 12 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGE ENGLISHChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Concept application exercise 5.2
Explore 8 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGE ENGLISHChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Archives (Numerical Value Type)
Explore 3 Videos
- PROGRESSION AND SERIESBook:CENGAGE ENGLISHChapter:PROGRESSION AND SERIESExercise:ARCHIVES (MATRIX MATCH TYPE )
Explore 1 Video
- RELATIONS AND FUNCTIONSBook:CENGAGE ENGLISHChapter:RELATIONS AND FUNCTIONSExercise:Archives(Matrix Match Type)
Explore 1 Video
Similar Questions
Find the value of a2+b2+c2R2 in any right-angled triangle.
View SolutionIf the sides of a triangle are a, b and √a2+ab+b2, then find the greatest angle
View SolutionLet ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
View SolutionMatch the statements /expression given in List I with the values given in List II.

View SolutionLet E1={x∈R:x≠1andxx−1>0}andE2={x∈E1:sin−1(loge(xx−1)) is real number}
(Here, the inverse trigonometric function sin−1x assumes values in [−π2,π2].)
Let f:E1→R be the function defined by f(x)=loge(xx−1)andg:E2→R be the function defined by g(x)=sin−1(loge(xx−1)).

The correct option is
View SolutionIn Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such thatAD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).

View SolutionABCD is a trapezium with AB II DC and M, N are points on AD and BC such that MN ll DC. If the area of ABNM is half the area of ABCD, then x^2= ? N (A) a+b (B) a^2+ b^2 (C)(a^2+b^2)/2 (D) none of these RF 9cm, CF 12cm, if BE is perpendicular to CF, then
View SolutionABCD is a trapezium such that AB and CD are parallel and BC⊥CD . If ∠ADB=θ,BC=pandCD=q , then AB is equal to (1) p2+q2cosθpcosθ+qsinθ (2) p2+q2p2cosθ+q2sinθ (3) (p2+q2)sinθ(pcosθ+qsinθ)2 (4) (p2+q2)sinθpcosθ+qsinθ
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that AP bisects \ ∠A as well as ∠D AP is the perpendicular bisector of BC
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionIf AB is a chord of a circle, Pand Q are the two points on the circle different from A and B, then ∠APB= ∠AQB ∠APB+∠AQB=180∘ or∠APB= ∠AQB
View SolutionIf psinθ+qcosθ=aandpcosθ−qsinθ=b, show that : p+aq+b+q−bp−a=0.
View SolutionIn Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such thatAD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).
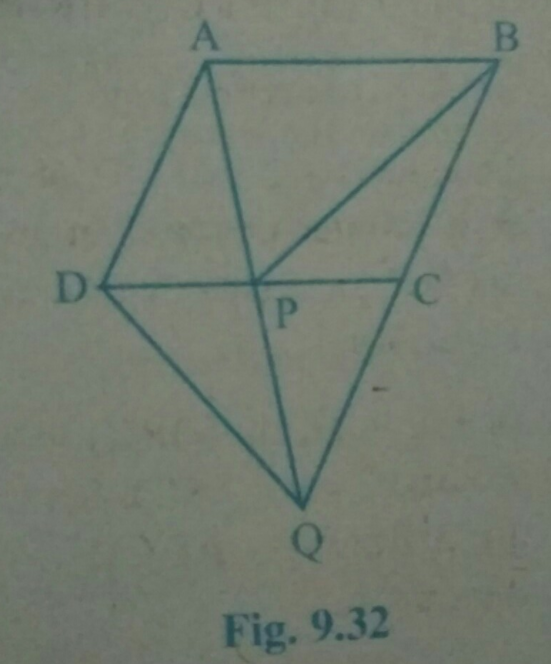
View SolutionIf a,b,andc are in A.P. p,q,andr are in H.P., and ap,bq,andcr are in G.P., then pr+rp is equal to a/c+c/a
View SolutionIf a,b,andc are in A.P. p,q,andr are in H.P., and ap,bq,andcr are in G.P., then pr+rp is equal to ac−ca b. ac+ca c. bq+qb d. bq−qb
View SolutionIf a,b,andc are in A.P. p,q,andr are in H.P., and ap,bq,andcr are in G.P., then pr+rp is equal to ac−ca b. ac+ca c. bq+qb d. bq−qb
View Solution
