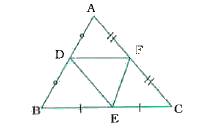
D, E and F are the mid-points of AB, BC and CA of the equilateral ΔABC. Prove that ΔDEF is also an equilateral triangle.Solution in Bengali
Step by step video & image solution for D, E and F are the mid-points of AB, BC and CA of the equilateral DeltaABC. Prove that DeltaDEF is also an equilateral triangle. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
D, E and F are the mid-points of the sides AB, BC and CA of the ΔABC. Prove that ΔDEF=14ΔABC.
View SolutionABC is a triangle and D,E,F are the mid-points of the sides BC,CA, AB respectively . The ratio of the areas of ΔABCandΔDEF is :
View SolutionD, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral ΔABC. Show that ΔDEF is also an equilateral triangle.
View SolutionD, E and F are respectively the mid-points of sides AB, BC and CA of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC.
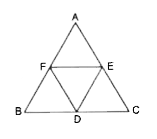
View Solutionआकृति में एक समबाहु त्रिभुज ABC की भुजाओं BC,CA तथा AB के मध्य-बिंदु क्रमशः D,E तथा F हैं, तो सिद्ध करें कि ΔDEF भी एक समबाहु त्रिभुज हैं।
View SolutionD, E and F are the mid-points of the sides AB, BC and CA of an isosceles triangle ABC in which AB = BC. Prove that ΔDEF is also isosceles.
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB of the equilateral ΔABC. Prove that ΔDEF is also an equilateral triangle.

View Solution
