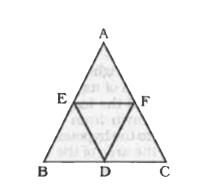
In Figure, D,E
and F
are, respectively the mid-points of sides BC,CA
and AB
of an equilateral triangle ABC
. Prove that DEF
is also an equilateral triangle.


Pr∞f:AsABCisanequilateral△<br>therefore AB=BC=AC−(1)<br>Bym∮theorem:<br>EF=1/2 BC <br>DF=1/2 AC<br>DE=1/2 AB<br>therefore 1/2 AB=1/2 AC=1/2 BC<br>therefore EF=DF=ED<br>Sinceallthessof/_\DEF are equal, DEF is an equilateral triangle
Similar Questions
In Figure, D,E and F are, respectively the mid-points of sides BC,CA and AB of an equilateral triangle ABC . Prove that DEF is also an equilateral triangle.
View Solutionlf D, E and F are respectively the midpoints of the sides BC, CA and AB of an equilateral triangle ABC, prove that △DEF is also an equilateral triangle.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB, respectively of and equilateral ΔABC. Show that ΔDEF is also an equilateral triangle.
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB of the equilateral ΔABC. Prove that ΔDEF is also an equilateral triangle.

View SolutionIf D, E and F are the mid-points of the sides of an equilateral triangle ABC, then the ratio of the area of triangle DEF and DCF is :
View SolutionIn the adjoining figure D, E and F are the mid - points of the sides BC, AC and AB respectively to triangle. Show that ∠EDF=∠A, ∠DEF=∠B and ∠DFE=∠C:

View SolutionE,F,G,H are respectively, the mid-points of the sides AB,BC,CD and DA of parallelogram ABCD . Show that the quadrilateral EFGH is a parallelogram and that its area is half the area of the parallelogram, ABCD. GIVEN : A quadrilateral ABCD in which L,F,G,H are respectively the mid-points of the sides AB,BC,CD and DA. TO PROVE : (i) Quadrilateral EFGH is a parallelogram ar(^(gm)EFGH)=12ar(^(gm)ABCD) CONSTRUCTION : Join AC and HF
View SolutionIf D,E,F are the mid-points of the sides BC,CAandAB respectively of a triangle ABC, prove by vector method that AreaofDEF=14(areaofABC).
View SolutionIn ΔABC, D, E and F are respectively the mid-points of sides AB, BC and CA. Show that ΔABCis divided into four congruent triangles by joining D, E and F.
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, AC and AB respectively. △DEF is congruent to triangle :

View Solution