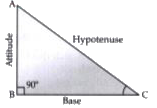
ΔABC is a right triangle, right angled at B. ∠C is a given acute angle. So side BC is base, a side AB is altitude and side AC is hypotenuse for given acute angle C.
HypotenuseAltitude is equal to ______
tan C
sin C
sec C
cosec C
The correct Answer is:D
Step by step video solution for DeltaABC is a right triangle, right angled at B. angleC is a given acute angle. So side BC is base, a side AB is altitude and side AC is hypotenuse for given acute angle C. ("Hypotenuse")/("Altitude") is equal to ______ by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023টপার এই প্রশ্নগুলো সমাধান করেছে
- INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES Book:OSWAL PUBLICATIONChapter:INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES Exercise:NCERT CORNER (Textbook Questions) (Exercise - 8.1)
Explore 18 Videos
- INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES Book:OSWAL PUBLICATIONChapter:INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES Exercise:NCERT CORNER (Textbook Questions) (Exercise - 8.2)
Explore 15 Videos
- INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES Book:OSWAL PUBLICATIONChapter:INTRODUCTION TO TRIGONOMETRY AND TRIGONOMETRIC IDENTITIES Exercise:SELF ASSESSMENT - 2 (I. Objective Type Questions)(IV.Long Answer Type Questions - II)
Explore 3 Videos
- INTRODUCTION TO TRIGONOMETRY Book:OSWAL PUBLICATIONChapter:INTRODUCTION TO TRIGONOMETRY Exercise:Self - Assessment
Explore 15 Videos
- LINES (IN TWO - DIMENSIONS)Book:OSWAL PUBLICATIONChapter:LINES (IN TWO - DIMENSIONS)Exercise:BOARD CORNER (LONG ANSWER TYPE QUESTION)
Explore 2 Videos
সম্পর্কিত প্রশ্ন
In ΔABC , right - angled at B , AB = 24 cm , BC = 7 cm .
sinA,cosA
View SolutionEvalulate the following :
sin60∘cos30∘+sin30∘cos60∘
View SolutionProve that tan2Atan2A−1+cosec2Asec2A−cosec2A=11−2cos2A
View SolutionIn ΔABC right - angled at c, AB = 29 units BC = 21 units and ∠ABC=θ Determine the value of
cos2θ+sin2θand
View SolutionIf a≠b≠c,prove that(a,a2),(b,b2),(0,0) will not be collinear.
View SolutionIn a right angled triangle with sides a and b and hypotenuse c , the altitude drawn on the hypotenuse is x . Prove that ab=cx .
View SolutionIn a right angled with sides a and b and hypotenuse c, the altitude drawn on the hypotenuse is x. prove that ab=cx.
View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe area of a right angled triangle is 24 cm and one of the sides containing the right angle is 6 cm. The altitude on the hypotenuse is
View SolutionIn a right angled triangle with sides a and b and hypotenuse c , the altitude drawn on the hypotenuse is x . Prove that ab=cx .
View SolutionThe sum of the hypotenuse and a side of a right angled triangle is constant . If the area of the triangle is maximum then the angle between the hypotenuse and the given side is
View SolutionIf hypotenuse and an acute angle of one right triangle are equal to the hypotenuse and an acute angle of another right triangle, then the triangles are congruent
View SolutionIf A be the area of a right triangle and b one of the sides containing the right angle, prove that the length of the altitude on the hypotenuse is 2AB√b4+4A2
View SolutionIn a right-angled triangle, the square of the hypotenuse is equal to twice the product of the other two sides. One of the acute angles of the triangle is
View Solution