If 2x−y+1=0 is a tangent to the hyperbola x2a2−y216=1 then which of the following CANNOT be sides of a right angled triangle?
2a,8,1
a,4,1
a,4,2
2a,4,1
The correct Answer is:A, B, C
Step by step video solution for If 2x-y+1=0 is a tangent to the hyperbola (x^2)/(a^2)-(y^2)/(16)=1 then which of the following CANNOT be sides of a right angled triangle? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HYPERBOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - HYPERBOLAEXERCISE - Hyperbola Exercise 11 : Questions Asked in Previous 13 Years Exams
3 Videos
- HYPERBOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - HYPERBOLAEXERCISE - Hyperbola Exercise 10 : Subjective Type Questions
3 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
10 Videos
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHS ENGLISHCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
Similar Questions
Matching the information given in the three columns of the following table column 1, 2 and 3 contain conics, equations of tangents in the conics and points of contact, respectively.
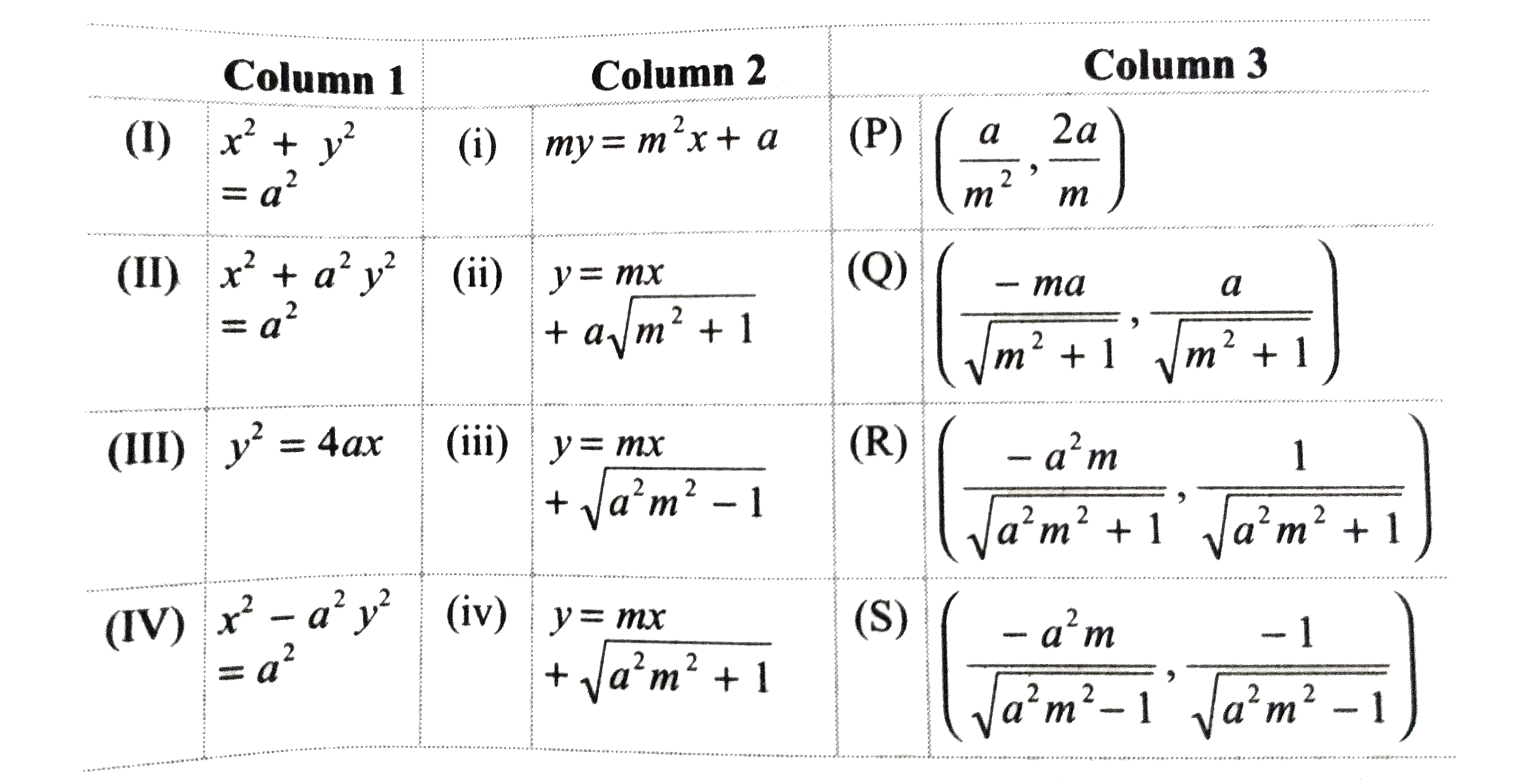
Q. The tangent to a suitable conic (column 1) at (√3,12) is found to be √3x+2y=4, then which of the following options is the correct combination?
View SolutionIf there are two points A and B on rectangular hyperbola xy=c2 such that abscissa of A =ordinate of B, then the locus of points of intersection of tangents at A and B is
View SolutionFind the number of solutions of the equation x21−|x−2|=1, graphically.
View SolutionThe integral ∫sec2x(secx+tanx)92dx equals (for some arbitrary constant K). −1(secx+tanx)112{111−17(secx+tanx)2}+K 1(secx+tanx)111{111−17(secx+tanx)2}+K −1(secx+tanx)112{111+17(secx+tanx)2}+K 1(secx+tanx)112{111+17(secx+tanx)2}+K
View SolutionIf 2x−y+1=0 is a tangent to the hyperbola x2a2−y216=1 then which of the following CANNOT be sides of a right angled triangle? (a)a,4,2 (b) a,4,1 (c)2a,4,1 (d) 2a,8,1
View SolutionIf 2x−y+1=0 is a tangent to hyperbola x2a2+y216=1, then which of the following are sides of a right angled triangle ?
View SolutionThe slopes of the common tangents of the hyperbolas x29−y216=1 and y29−x216=1, are
View SolutionThe area of triangle formed by the lines x−y=0,x+y=0 and any tangent to the hyperbola x2−y2=16 is equal to
View Solutionयदि 2x−y+1=0 अतिपरवलय x2a2−y216=1 की स्पर्शरेखा है तो निम्न में से कौनसी समकोणीय त्रिभुज की भुजायें नहीं हो सकती है (हैं)
View Solutionअतिपरवलय x29−y216=1 तथा y29−x216=1 की उभयनिष्ठ स्पर्श रेखा की प्रवणता है
View SolutionIf 3x+2y−1=0 is a tangent to a hyperbola x216−y29=1, then the point of contact is
View SolutionHyperbola x^2/(25)-y^2/(16)=1 The line that follows 2x+y=1 Is perpendicular to, the equation of is
View SolutionIf 2x−y+1=0 is a tangent to the hyperbola x2a2−y216=1 then which of the following CANNOT be sides of a right angled triangle?
View Solutionआकृति में यदि ABIICD,∠APQ=50∘और∠PRD=127∘ है, तो Y का मान है-
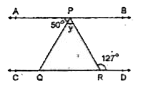
View Solutionयदि 2x−y+1=0 अतिपरवलय x2a2−y216=1 की स्पर्शरेखा है तो निम्न में से कौनसी समकोणीय त्रिभुज की भुजायें नहीं हो सकती है (हैं)
View SolutionTangents drawn from a point on the circle x2+y2=9 to the hyperbola x225−y216=1,
then tangents are at angle
View Solution

