In Fig. 6.44, the side QR of
PQR is produced to a point S. If the bisectors of ∠PQR\ and∠PRS
meet at point T, then prove that ∠QTR=12∠QPR
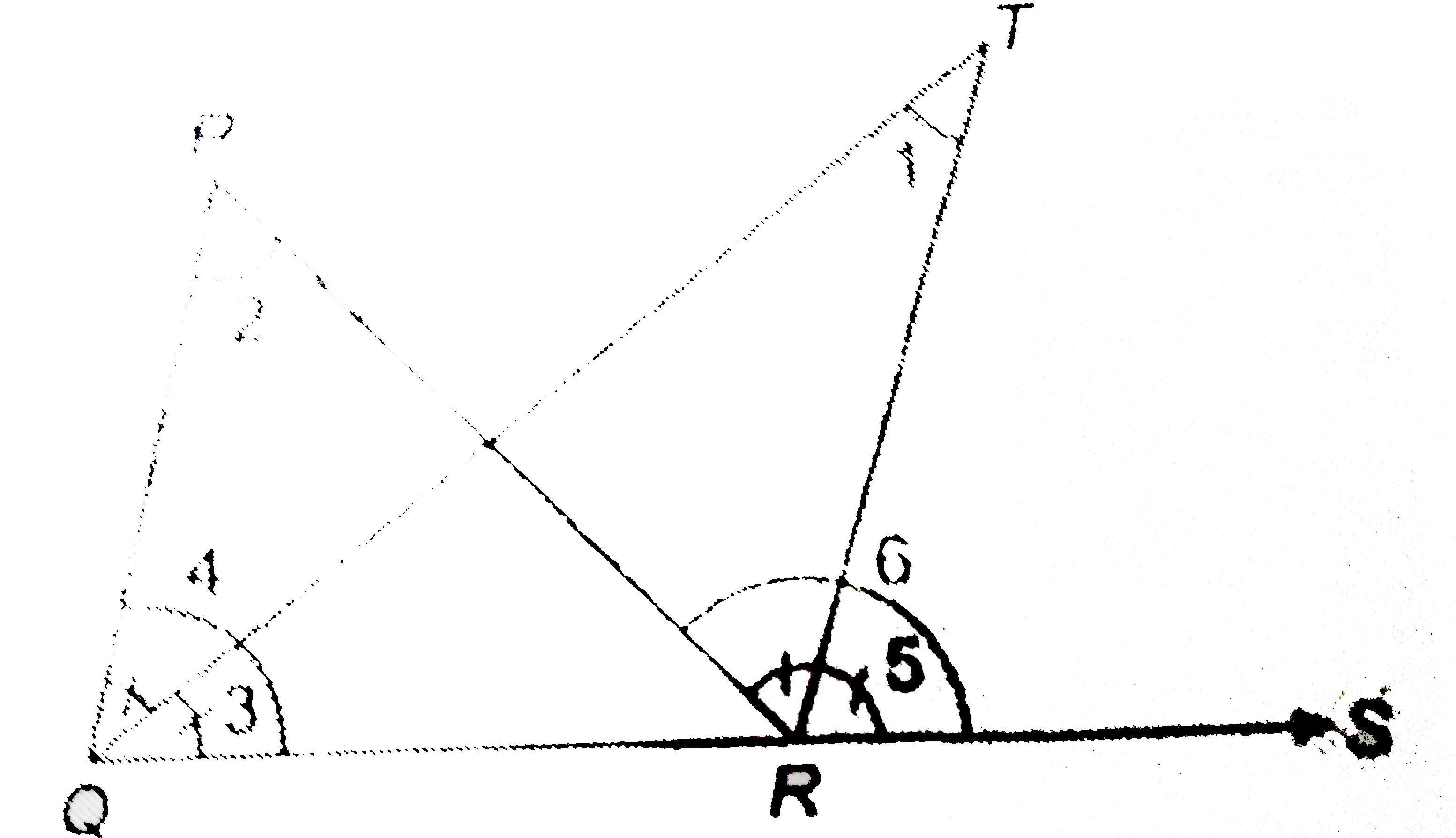 .
.
∠5=12∠6 ( ∴ RT is the bisector of ∠PRS)

=12(∠+∠4) ( ∴ exterior angle is equal to the sum of opposite interior angels)......(1)
Also, ∠5=∠1+∠3 ( exterior angle is equal to the sum of opposite interior angels)......(2)
From (1) and (2), we get
∠1+12∠4=12(∠2+∠4) (each is equal to ∠5)
⇒∠1+12∠4=12∠2+12∠4
⇒∠1=12∠2
Topper's Solved these Questions
- LINES AND ANGLESBook:NAGEEN PRAKASHANChapter:LINES AND ANGLESExercise:Exercise 6 A
Explore 19 Videos
- LINES AND ANGLESBook:NAGEEN PRAKASHANChapter:LINES AND ANGLESExercise:Exercise 6 B
Explore 16 Videos
- LINES AND ANGLESBook:NAGEEN PRAKASHANChapter:LINES AND ANGLESExercise:Revision Exercise (long Answer Questions )
Explore 6 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBook:NAGEEN PRAKASHANChapter:LINEAR EQUATIONS IN TWO VARIABLESExercise:Revision Exercise
Explore 12 Videos
- NUMBER SYSTEMBook:NAGEEN PRAKASHANChapter:NUMBER SYSTEMExercise:Revision Exercise (short Answer Questions)
Explore 10 Videos
Similar Questions
Two angles are in the ratio 4:5 Find the angles if they are (i) complementary (ii) supplementary to each other.
View SolutionIf AB ||CD in each of the following find x

View SolutionIf two parallel lines intersected by a transversal; prove that the bisectors of the two pairs of interior angle encloses a rectangle.
View SolutionWrite the equation of x axis.
View SolutionFind two rational numbers between −14and25.
View SolutionIn Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.

View SolutionIn Fig. 6.31, if PQ∣∣ST,∠PQR=110∘ and∠RST=130∘, find ∠QRS.

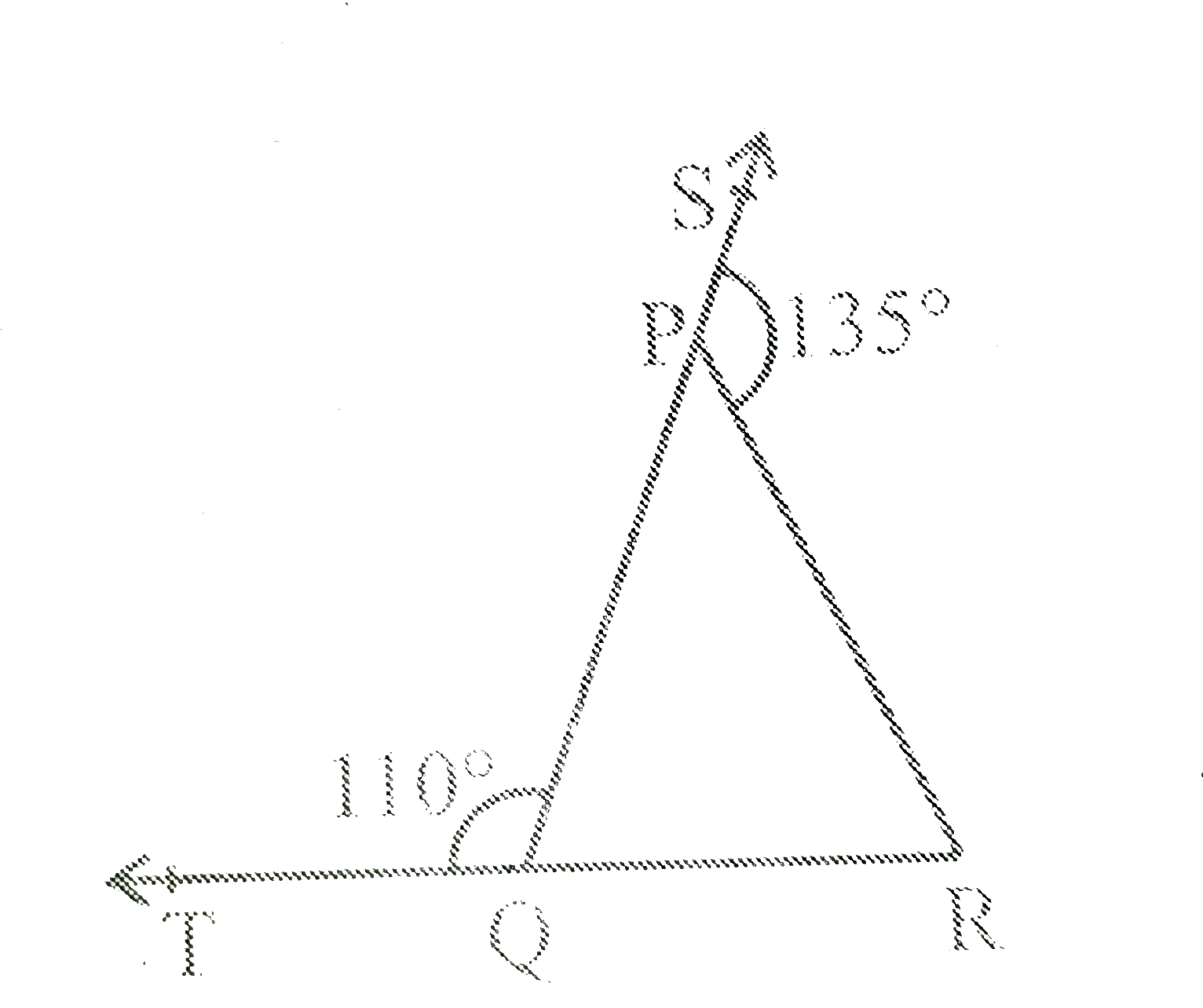
View SolutionIn Fig. 6.39, sides QP and RQ of ΔPQR are produced to point S and T respectively. If ∠SPR=135∘ and ∠PQT=110∘, find ∠PRQ.
View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.

View SolutionIn Fig 7.51, PR > PQand PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.

View SolutionIn Figure, PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. Prove that ∠R> ∠P and ∠S> ∠Q Given : PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. To Prove : (i) ∠R> ∠P (ii) ∠S> ∠Q Construction : Joint PR and QS
View Solutionआकृति 6.44 में, ΔPQR की भुजा QR को बिदु ऽ तक बढ़ाया गया है । यदि ∠PQR और ∠PRS के समद्विभाज़क बिन्दु T पर मिलते है, तो सिद्ध कीजिये की ∠QTR=12∠QPR

View SolutionIn Fig. , the side QR of △ PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.

View SolutionIn Fig. 6.31, if PQ∣∣ST,∠PQR=110∘ and∠RST=130∘, find ∠QRS.

View SolutionIn Fig. 6.39, sides QP and RQ of ΔPQR are produced to point S and T respectively. If ∠SPR=135∘ and ∠PQT=110∘, find ∠PRQ.

View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.

View Solution