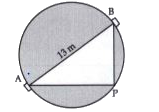
In the Dwarika residency colony, there is a circular park of diameter 13 metres. A pole has to erected at the point P on the boundary of circular park in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres.
For equation, ax2+bx+c=0,b2−4ac is called the .....
Discriminant
Distinct roots
Quadratic equation
None of these
Step by step video solution for In the Dwarika residency colony, there is a circular park of diameter 13 metres. A pole has to erected at the point P on the boundary of circular park in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. For equation, ax^(2) + bx + c=0, b^(2)-4ac is called the ..... by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRATIC EQUATIONSBook:OSWAL PUBLICATIONChapter:QUADRATIC EQUATIONSExercise:SELF ASSESSMENT -2 (Multiple Choice Questions:)
Explore 3 Videos
- QUADRATIC EQUATIONSBook:OSWAL PUBLICATIONChapter:QUADRATIC EQUATIONSExercise:SELF ASSESSMENT -2 (Fill in the Blanks:)
Explore 3 Videos
- QUADRATIC EQUATIONSBook:OSWAL PUBLICATIONChapter:QUADRATIC EQUATIONSExercise:SELF ASSESSMENT -1 (Long Answer Type Questions-III)
Explore 2 Videos
- PROBABILITYBook:OSWAL PUBLICATIONChapter:PROBABILITYExercise:Self Assessment
Explore 66 Videos
- REAL NUMBERSBook:OSWAL PUBLICATIONChapter:REAL NUMBERSExercise:Self-Assessment
Explore 11 Videos
Similar Questions
The value of p for which the quadratic equation 4x2+px+3=0 has equal roots are.
View SolutionNature of roots of quadratic equation 4x2+3x−14=0 is…..
View SolutionGiven, solve for x:(2xx−5)2+5(2xx−5)−24=0,x≠5
View SolutionA bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball from the bag is double that of a red ball, find the number of blue balls in the bag.
View SolutionFind the H.C.F. of x2+3x–10andx3−8x.
View SolutionA pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it possible to do so? If yes, at what distances from the two gates should the pole be erected?
View SolutionA pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it the possible to do so? If yes, at what distances from the two gates should the pole be erected?
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionA pole has to be erected at a point on the boundary of a circular ground of diameter 20m in such a way that the difference of its distance form two diameterically opposite fixed gates P and Q on the boundary is 4 m. Is it possible to do so? If answer is yes at what distance from the two gates should the pole be erected?
View SolutionA pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences opposite fixed gates A and B on the boundary is 7 metres. Is it possible to do so ? If yes, at what distances from the two gates should the pole be erected ?
View Solution13 cm. It was intended to erect a pillar on the boundary of a circular park of diameter. The distance from the two gates A and B, which are arranged opposite the boundary of the park, i.e. at the end points of a diameter, to this pillar is 7 m. Can the pillar be set up as it is? If so, how far is this pillar from the two gates?
View SolutionOne root of the equation x2+ax+3=0 is 1.Find the value of a.
View SolutionA pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it possible to do so? If yes, at what distances from the two gates should the pole be erected?
View SolutionA pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it possible to do so? If yes, at what distances from the two gates should the pole be erected?
View SolutionA pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it possible to do so? If yes, at what distances from the two gates should the pole be erected?
View Solution