In the figure , O is the centre of the circle and BCD is tangent to it at C . Find the value of ∠BAC+∠ACD

A
90∘
B
80∘
C
45∘
D
60∘
Text Solution
The correct Answer is:A
|
Topper's Solved these Questions
- TANGENTS TO CIRCLES Book:CENGAGEChapter:TANGENTS TO CIRCLES Exercise:OLYMPIAD AND NTSE LEVEL EXERCISES
Explore 10 Videos
- TANGENTS TO CIRCLES Book:CENGAGEChapter:TANGENTS TO CIRCLES Exercise:TEST YOURSELF (LEVEL 2)
Explore 4 Videos
- STANDARD AND ALLIED ANGLESBook:CENGAGEChapter:STANDARD AND ALLIED ANGLESExercise:Olympiad And NTSE Level Exercises
Explore 10 Videos
- TRANSFORMATIONSBook:CENGAGEChapter:TRANSFORMATIONSExercise:Olympiad and NTSE level exercises
Explore 10 Videos
Similar Questions
Knowledge Check
In the figure, O is the centre of a circle and AT is a tangent at point A. The measure of ∠BAT is:
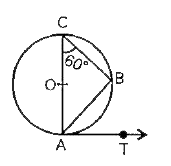 A30∘B60∘C75∘D105∘
A30∘B60∘C75∘D105∘In the given figure , O is the centre of the circle . AP and AQ are tangents to the circle .∠PRQ=
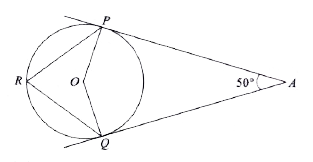 A55∘B45∘C75∘D65∘
A55∘B45∘C75∘D65∘In the adjoining figure , O is the centre of the circle and ∠OAB=60∘. Find ∠APC.
 A=60∘B=45∘C=30∘D=50∘
A=60∘B=45∘C=30∘D=50∘
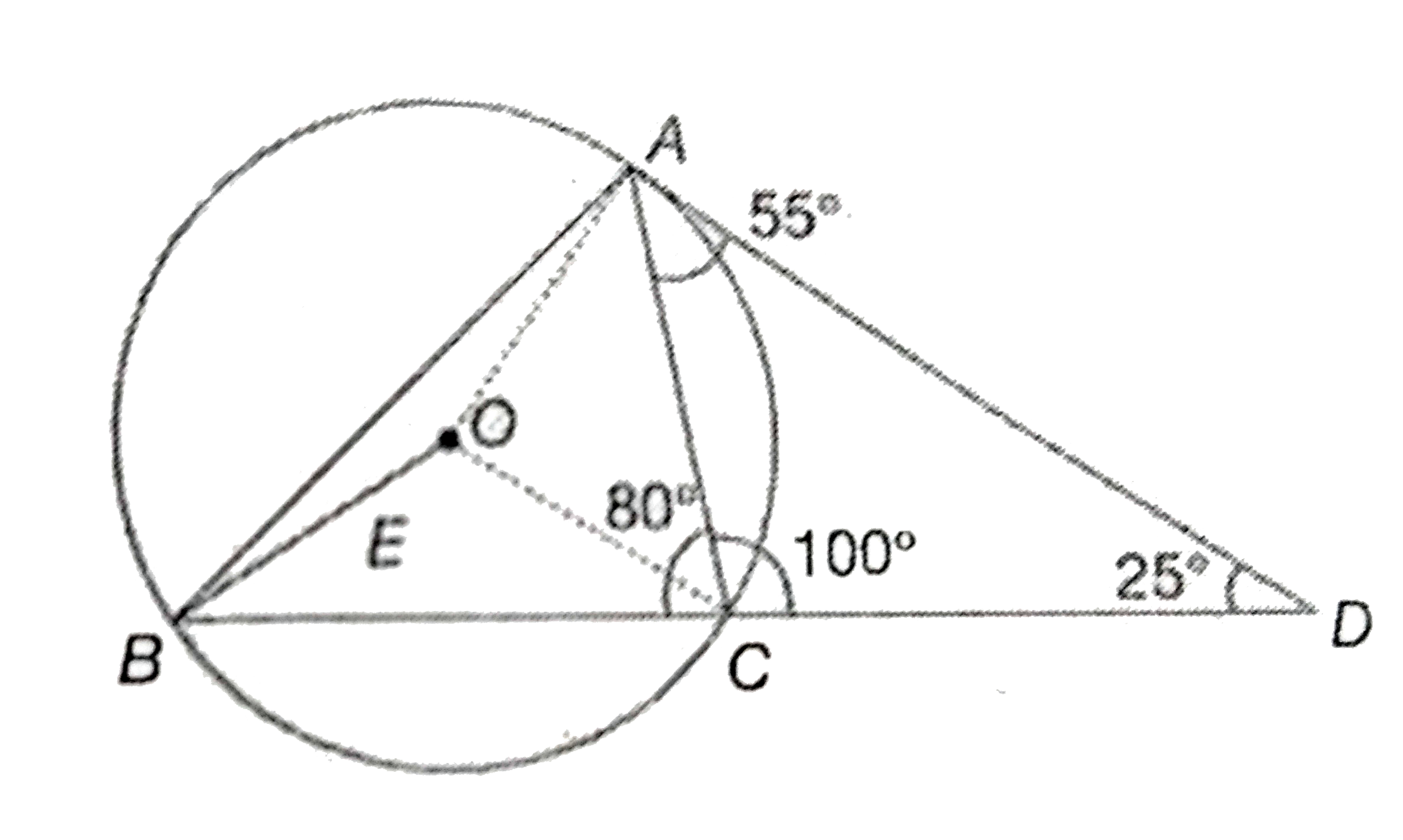
In the given, figure , O is the centre of the circle and AD is a tangent to the circle at.A if ∠CAD=55∘ and ∠ADC=25∘, then find ∠ABO.
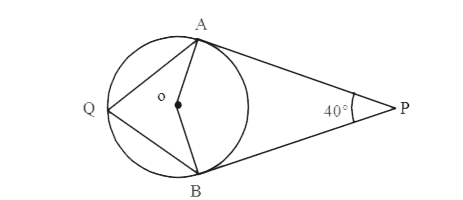
View SolutionIn the given figure, O is the centre of the circle, PA and PB are tangents to the circle then find ∠AQB.
View SolutionIn the given figure, O is the centre of a circle and ∠ADC=130∘.If ∠BAC=x∘, Find the value of x.

View SolutionIn the given figure, O is the centre of a circle and ∠ADC=130∘.If ∠BAC=x∘, Find the value of x.

View SolutionIn the adjoining figure , O is the centre of the circle and ∠OAB=60∘. Find ∠APC.

View Solution

