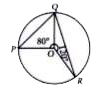
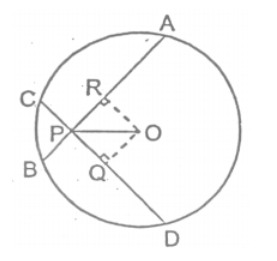
In the given figure, O is the centre of a circle C(O,r) and PO bisects ∠APC . Prove that AB=CD.
Video Solution
Text Solution
Draw OE⊥AB and OF⊥CD.
Now, in ΔOEP and ΔOFP we have
∠OEP=∠OFP [ each equal to 90∘]
∠OPE=∠OPF[ given ]
OP=OP [common]
∴ΔOEP≅ΔOFP[ AAS-congruence ]
⇒OE=OF [c.p.c.t.]
⇒ chords AB and CD are equidistnat from the centre O
⇒AB=CD [ chords equidistant from the centre are equal ].
Hence, AB=CD
|
Topper's Solved these Questions
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:Exercise 12A
Explore 22 Videos
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:EXERCISE 12B
Explore 18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBook:RS AGGARWALChapter:BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONExercise:EXERCISE 17B
Explore 16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Multiple Choice Questions (Mcq)
Explore 20 Videos
Similar Questions
Knowledge Check
In the given figure, O is the centre of the circle. The value of x is
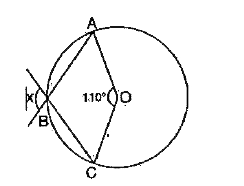 A75∘B55∘C125∘D110∘
A75∘B55∘C125∘D110∘In the given figures, value of y (O is the centre of the circle) is
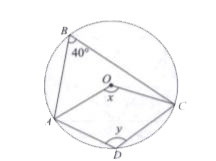 A100∘B120∘C130∘D140∘
A100∘B120∘C130∘D140∘
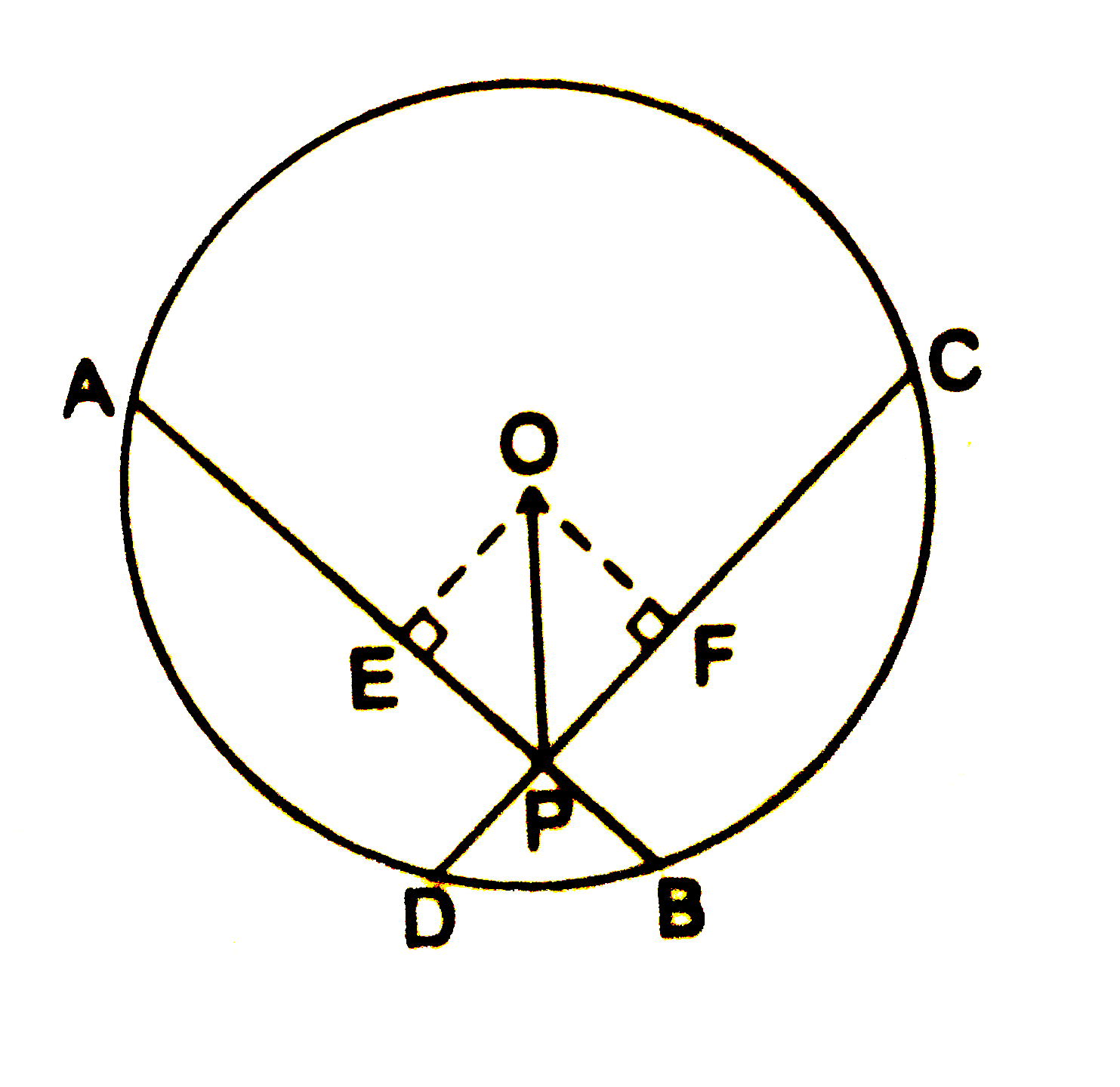
In Figure, O is the center of a circle and PO bisects ∠APD Prove that AB=CD
View SolutionIn Figure, AB=CB and O is the centre of the circle. Prove that BO bisects ∠ABC.
View SolutionIn a given figure, O is centre of circle then ∠x+∠y = ?
View SolutionIn the adjoining figure, O is the centre of a circle in which AB and CD are two diameters. Prove that AC| |BD and AD| |BC. If ∠OBD=50∘, then find the value of ∠AOC.

View SolutionIn the given figure. AB∣CDandO is the midpoint of AD.
View SolutionIn the given figure, O is the centre of a circle such that OA = 5 cm, AB = 8 cm and OD⊥AB meeting AB at C. Find the length of CD.
View Solution