In triangle ABC, D is a point in side BC such that 2BD=3DC. Prove that the area of triangle ABD = 35×Area ofΔABC
To prove that the area of triangle ABD is 35 times the area of triangle ABC, we can follow these steps:
Step 1: Understand the relationship between segments BD and DC
Given that 2BD=3DC, we can express the lengths of BD and DC in terms of a common variable. Let BD=x. Then, DC can be expressed as:
DC=23BD=23x
Step 2: Find the total length of BC
Now, we can find the total length of BC:
BC=BD+DC=x+23x=33x+23x=53x
Step 3: Express BD in terms of BC
From the equation BC=53x, we can express x (which is BD) in terms of BC:
BD=35BC
Step 4: Calculate the area of triangle ABD
The area of triangle ABD can be calculated using the formula for the area of a triangle:
Area of △ABD=12×base×height
Here, the base is BD and the height is the perpendicular distance from A to line BC, which we can denote as AM:
Area of △ABD=12×BD×AM
Step 5: Substitute BD in the area formula
Substituting BD=35BC into the area formula gives:
Area of △ABD=12×(35BC)×AM
=310BC×AM
Step 6: Calculate the area of triangle ABC
The area of triangle ABC can also be expressed using the same height AM:
Area of △ABC=12×BC×AM
Step 7: Relate the areas of triangles ABD and ABC
Now, we can relate the area of triangle ABD to the area of triangle ABC:
Area of △ABD=310BC×AM
Area of △ABC=12BC×AM
To express the area of triangle ABD in terms of the area of triangle ABC, we can write:
Area of △ABD=310×12BC×AM×53
=35×Area of △ABC
Conclusion
Thus, we have proved that:
Area of △ABD=35×Area of △ABC
Given that 2BD=3DC, we can express the lengths of BD and DC in terms of a common variable. Let BD=x. Then, DC can be expressed as:
DC=23BD=23x
Now, we can find the total length of BC:
BC=BD+DC=x+23x=33x+23x=53x
From the equation BC=53x, we can express x (which is BD) in terms of BC:
BD=35BC
The area of triangle ABD can be calculated using the formula for the area of a triangle:
Area of △ABD=12×base×height
Here, the base is BD and the height is the perpendicular distance from A to line BC, which we can denote as AM:
Area of △ABD=12×BD×AM
Substituting BD=35BC into the area formula gives:
Area of △ABD=12×(35BC)×AM
=310BC×AM
The area of triangle ABC can also be expressed using the same height AM:
Area of △ABC=12×BC×AM
Now, we can relate the area of triangle ABD to the area of triangle ABC:
Area of △ABD=310BC×AM
Area of △ABC=12BC×AM
To express the area of triangle ABD in terms of the area of triangle ABC, we can write:
Area of △ABD=310×12BC×AM×53
=35×Area of △ABC
Thus, we have proved that:
Area of △ABD=35×Area of △ABC
Topper's Solved these Questions
- AREA THEOREMSBook:ICSEChapter:AREA THEOREMSExercise:Exercies 16(A)
Explore 36 Videos
- AREA THEOREMSBook:ICSEChapter:AREA THEOREMSExercise:Exercies 16(B)
Explore 16 Videos
- AREA AND PERIMETER OF PLANE FIGURESBook:ICSEChapter:AREA AND PERIMETER OF PLANE FIGURESExercise:EXERCISE 20(D)
Explore 12 Videos
- CHAPTER REVISION (STAGE 2) Book:ICSEChapter:CHAPTER REVISION (STAGE 2) Exercise:DISTANCE FORMULA
Explore 12 Videos
Similar Questions
In an equilateral triangle ABC, D is a point on side BC such that BD=13BC. Prove that 9AD2=7AB2.
View SolutionThe base BC of triangle ABC is divided at D so that BD = 12 DC.
Prove that area of ΔABD=13 of the area of ΔABC.
View SolutionIn ΔABC,AB=ACandD is a point an side AC such that AD = BD = BC . Show that : ∠ADB=108∘
View SolutionIn the adjoining figure, D is the mid-point of side AB of ΔABC and P be any point on side BC. If CQ∣∣PD, then prove that:
area of ΔBPQ=12× area of ΔABC

View SolutionThe medians of ΔABC intersect at point G. Prove that:
area of ΔAGB=13× area of ΔABC
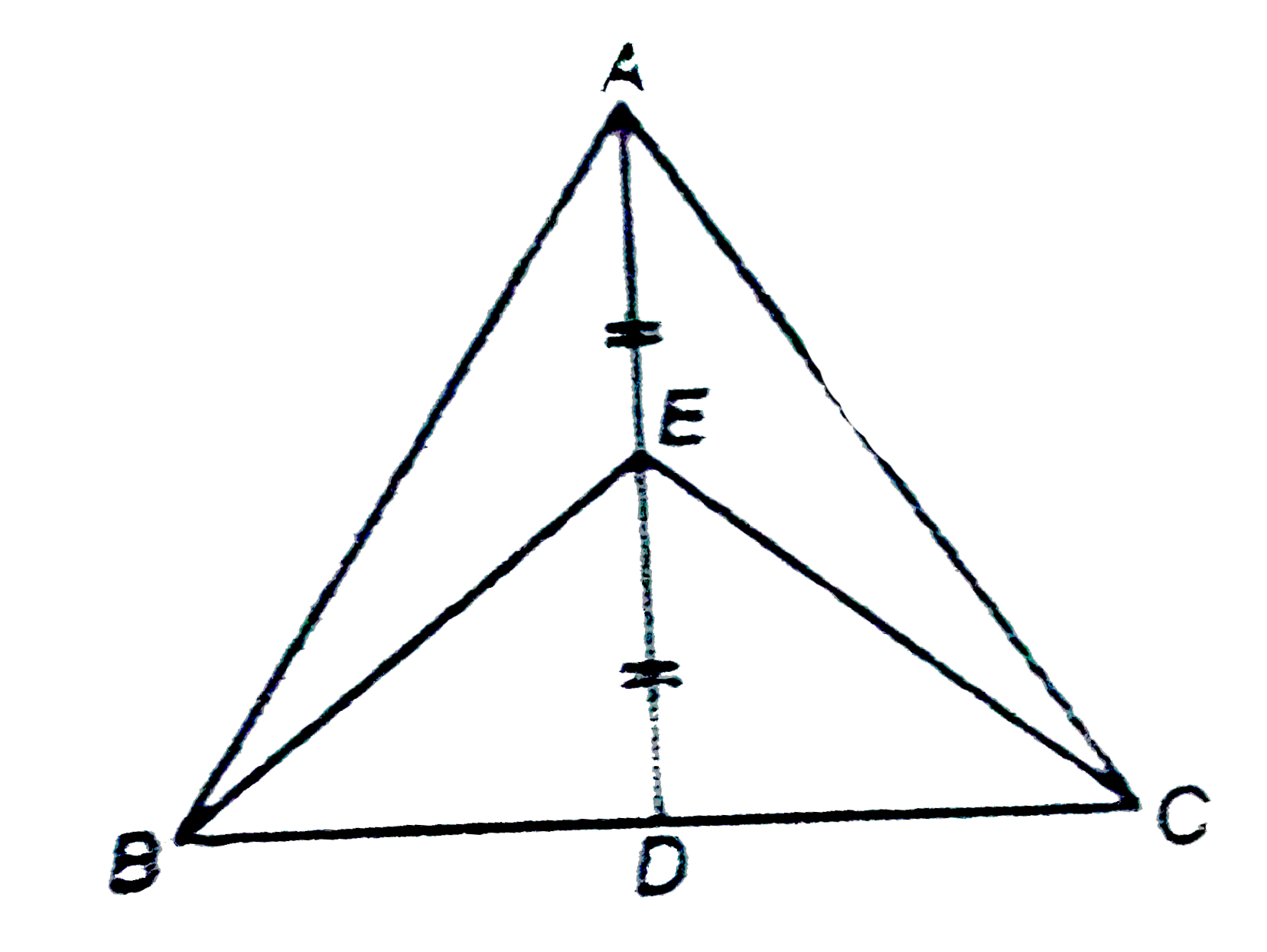
View SolutionIn the adjoining figure, BD = DC and AE = ED. Prove that
area of ΔACE=14 area of ΔABC
View SolutionAny point D is taken on the side BC of a ΔABC and AD is produced to E such that AD = DE , prove that area of ΔBCE= area of ΔABC,
View SolutionD is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that 8× area of (ΔAFD)= area of ΔABC
View SolutionIn a ΔABC, D is the mid point of side AC such that BD =12 AC. Show that ∠ABC is a right angle.
View SolutionIn triangles ABC , AD is perpendicular to BC and AD2=BD×DC . Prove that angle BAC=90∘
View Solution