Tangents are drawn to the hyperbola x29−y24=1 parallet to the sraight line 2x−y=1. The points of contact of the tangents on the hyperbola are (A) (92√2,1√2) (B) (−92√2,−1√2) (C) (3√3,−2√2) (D) (−3√3,2√2)
(92√2,1√2)
(−92√2,−1√2)
(3√3,−2√2)
(−3√3,2√2)
The correct Answer is:A, B
Step by step video solution for Tangents are drawn to the hyperbola x^2/9-y^2/4=1 parallet to the sraight line 2x-y=1. The points of contact of the tangents on the hyperbola are (A) (9/(2sqrt2),1/sqrt2) (B) (-9/(2sqrt2),-1/sqrt2) (C) (3sqrt3,-2sqrt2) (D) (-3sqrt3,2sqrt2) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HYPERBOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - HYPERBOLAEXERCISE - Hyperbola Exercise 11 : Questions Asked in Previous 13 Years Exams
3 Videos
- HYPERBOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - HYPERBOLAEXERCISE - Hyperbola Exercise 10 : Subjective Type Questions
3 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
10 Videos
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHS ENGLISHCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
Similar Questions
Matching the information given in the three columns of the following table column 1, 2 and 3 contain conics, equations of tangents in the conics and points of contact, respectively.
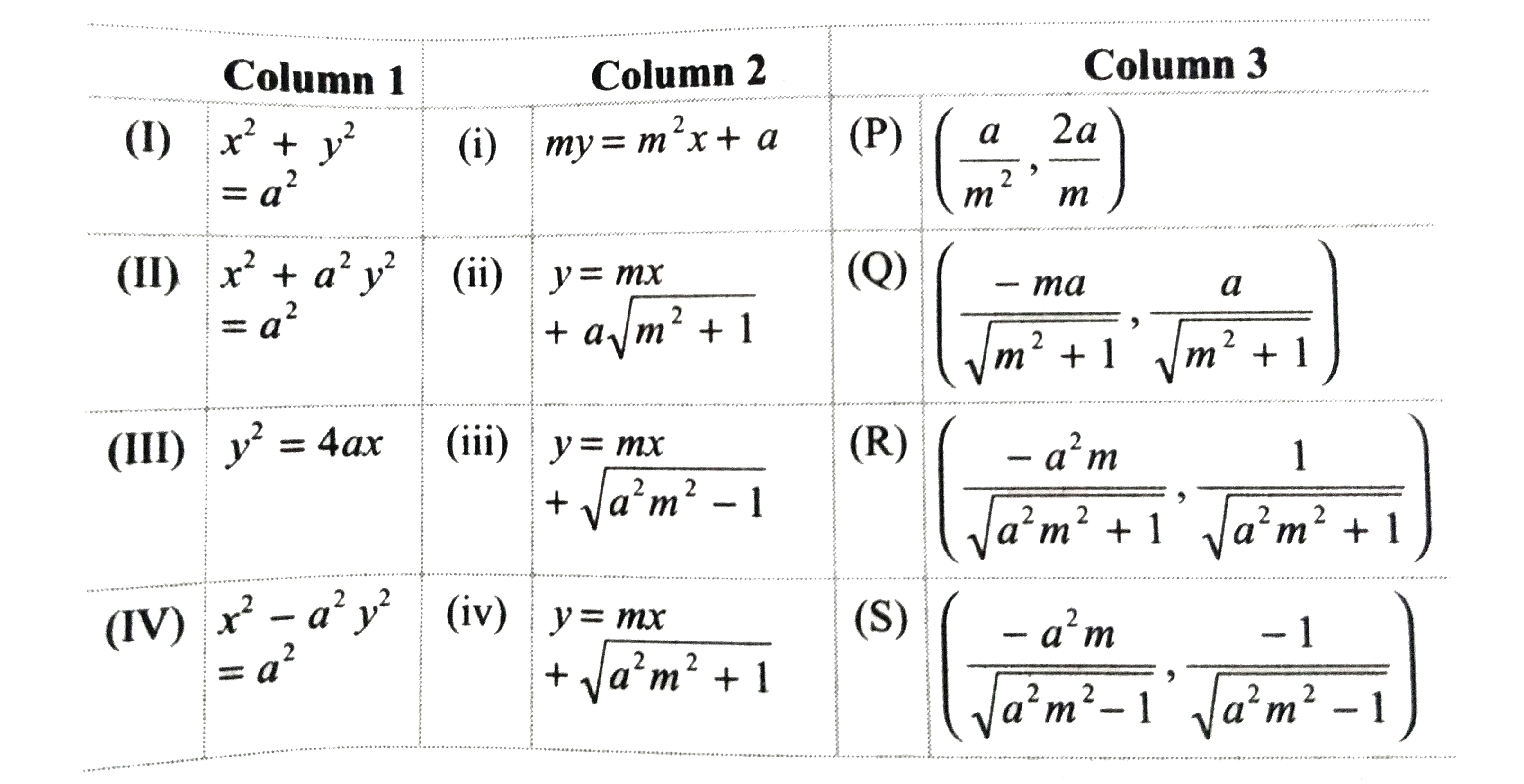
Q. The tangent to a suitable conic (column 1) at (√3,12) is found to be √3x+2y=4, then which of the following options is the correct combination?
View SolutionIf there are two points A and B on rectangular hyperbola xy=c2 such that abscissa of A =ordinate of B, then the locus of points of intersection of tangents at A and B is
View SolutionFind the number of solutions of the equation x21−|x−2|=1, graphically.
View SolutionThe integral ∫sec2x(secx+tanx)92dx equals (for some arbitrary constant K). −1(secx+tanx)112{111−17(secx+tanx)2}+K 1(secx+tanx)111{111−17(secx+tanx)2}+K −1(secx+tanx)112{111+17(secx+tanx)2}+K 1(secx+tanx)112{111+17(secx+tanx)2}+K
View SolutionTangents are drawn to the hyperbola (x^(2))/(9)-(y^(2))/(4)=1 parallet to the sraight line 2x-y=1. The points of contact of the tangents on the hyperbola are (A) ((2)/(2sqrt(2)),(1)/(sqrt(2)))(B)(-(9)/(2sqrt(3)),(1)/(sqrt(2)))(C)(3sqrt(3),-2sqrt(2))(D)(-3sqrt(3),2sqrt(2))
View SolutionTangents are drawn to the hyperbola x29−y24 parallel to the straight line 2x - y= 1 . One of the points of contact of tangents on the hyperbola is
View Solutionयदि सरल रेखा 2x−y=1 के समान्तर, x29−y24=1 अतिपरवलय पर स्पर्श रेखाएं जाती है, तो इन स्पर्श रेखाओं के अतिपरवलय पर स्पर्श बिन्दुहोंगे ।
View SolutionTangents are drawn to the hyperbol x^2/9-y^2/4=1 ,parallel to the straight line 2x - y = 1 . The points of contacts of the tangents of the hypebola are :
View SolutionTangents are drawn to the hyperbola x^2/9-y^2/4=1 parallet to the sraight line 2x-y=1. The points of contact of the tangents on the hyperbola are (A) (9/(2sqrt2),1/sqrt2) (B) (-9/(2sqrt2),-1/sqrt2) (C) (3sqrt3,-2sqrt2) (D) (-3sqrt3,2sqrt2)
View SolutionThe area enclosed by the curves y=sinx+cosxandy=|cosx−sinx| over the interval [0,π2] is (a) 4(√2−1) (b) 2√2(√2−1) (c) 2(√2+1) (d) 2√2(√2+1)
View Solution(1,2√2)is a point on circle, x2+y2=9. Which of the following is not the point on the circle at 2 units distance from (1,2√2)?
View Solutionयदि सरल रेखा 2x−y=1 के समान्तर, x29−y24=1 अतिपरवलय पर स्पर्श रेखाएं जाती है, तो इन स्पर्श रेखाओं के अतिपरवलय पर स्पर्श बिन्दुहोंगे ।
View SolutionWhat is the value of sin 15∘ ?................... A) √3−12√2 B) √3+12√2 C) 1−√32√2 D) 1+√3√2
View SolutionThe equation of normal to the curve y=2cosx at x=π4 is:
a)y−√2=2√2(x−π4)
b)y+√2=2√2(x+π4)
c)y−√2=1√2(x−π4)
d)y−√2=√2(x−π4)
View SolutionIf x(3√5+2√2)−√2(√10−1)y=√10(2√2+√5) then rational values of x and y are respectively___
View SolutionTangents are drawn to the hyperbola x^2/9-y^2/4=1 parallet to the sraight line 2x-y=1. The points of contact of the tangents on the hyperbola are (A) (2/(2sqrt2),1/sqrt2) (B) (-9/(2sqrt2),1/sqrt2) (C) (3sqrt3,-2sqrt2) (D) (-3sqrt3,2sqrt2)
View Solution

