The circle x2+y2−8x=0 and hyperbola x29−y24=1 intersect at points A and B.
The equation of a common tangent with positive slope to the circle as well as to the hperbola is
2x−√5y−20=0
2x−√5y+4=0
3x−4y+8=0
4x−3y+4=0
The correct Answer is:B
Step by step video solution for The circle x^(2)+y^(2)-8x=0 and hyperbola (x^(2))/(9)-(y^(2))/(4)=1 intersect at points A and B. The equation of a common tangent with positive slope to the circle as well as to the hperbola is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HYPERBOLABook:ARIHANT MATHS ENGLISHChapter:HYPERBOLAExercise:Hyperbola Exercise 11 : Questions Asked in Previous 13 Years Exams
Explore 3 Videos
- HYPERBOLABook:ARIHANT MATHS ENGLISHChapter:HYPERBOLAExercise:Hyperbola Exercise 10 : Subjective Type Questions
Explore 3 Videos
- GRAPHICAL TRANSFORMATIONSBook:ARIHANT MATHS ENGLISHChapter:GRAPHICAL TRANSFORMATIONSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 10 Videos
- INDEFINITE INTEGRAL Book:ARIHANT MATHS ENGLISHChapter:INDEFINITE INTEGRAL Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 8 Videos
Similar Questions
Matching the information given in the three columns of the following table column 1, 2 and 3 contain conics, equations of tangents in the conics and points of contact, respectively.
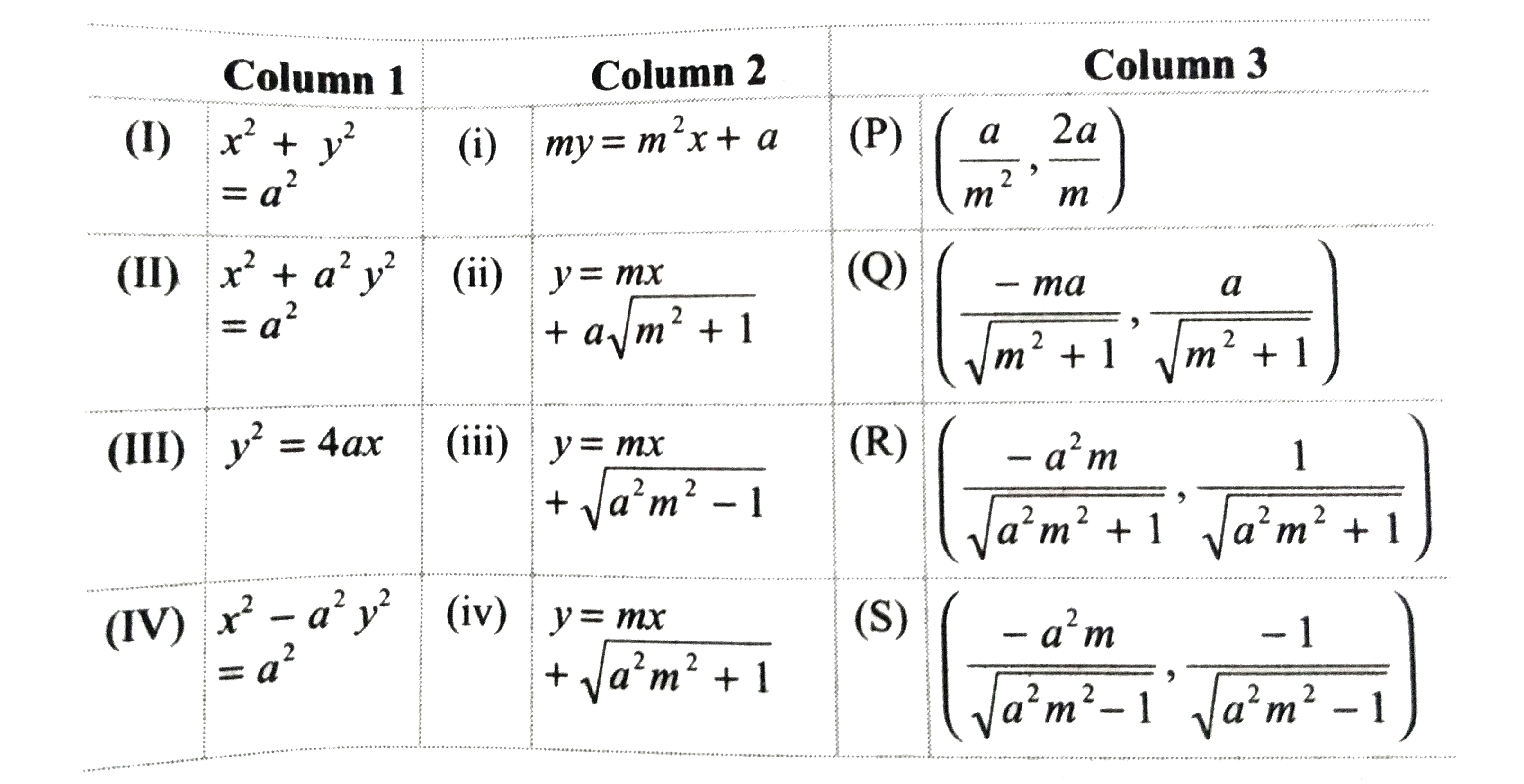
Q. The tangent to a suitable conic (column 1) at (√3,12) is found to be √3x+2y=4, then which of the following options is the correct combination?
View SolutionIf there are two points A and B on rectangular hyperbola xy=c2 such that abscissa of A =ordinate of B, then the locus of points of intersection of tangents at A and B is
View SolutionFind the number of solutions of the equation x21−|x−2|=1, graphically.
View SolutionThe integral ∫sec2x(secx+tanx)92dx equals (for some arbitrary constant K). −1(secx+tanx)112{111−17(secx+tanx)2}+K 1(secx+tanx)111{111−17(secx+tanx)2}+K −1(secx+tanx)112{111+17(secx+tanx)2}+K 1(secx+tanx)112{111+17(secx+tanx)2}+K
View SolutionThe circle x^(2)+y^(2)-8x=0 and hyperbola (x^(2))/(9)-(y^(2))/(4)=1 intersect at the points A and B Equation of the circle with AB as its diameter is
View SolutionThe circle x^(2)+y^(2)-8x=0 and hyperbola (x^(2))/(9)-(y^(2))/(4)=1 I intersect at the points A and B.Equation of a common tangent with positive slope to the circle as well as to the hyperbola is
View SolutionThe circle x2+y2−8x=0 and hyperbola x29−y24=1 intersect at points A and B. Then Equation of the circle with A B as its diameter is
View SolutionThe equation of a common tangent with negative slope to the circle x^(2)+y^(2)-8x=0 and the hyperbola 4x^(2)-9y^(2)=36 is
View SolutionThe circle x2+y2−8x=0 and hyperbola x29−y24=1 intersect at the points A and B. The equation of a common tangent with positive slope to the circle as well as to the hyperbola, is
View SolutionThe number of common tangents to the circles x2+y2=4,x2+y2−8x+12=0 is
View SolutionThe equation of the circle having the common chord of the circles x2+y2−8x=0 and x2+y2−9=0 as its diameter is
View Solutionवृत्तों x2+y2=4 तथा x2+y2−8x+12=0 के उभयनिष्ठ स्पर्श रेखाएँ हैं
View SolutionThe circle x2+y2−8x=0 and hyperbola x29−y24=1 I intersect at the points A and B. Equation of a common tangent with positive slope to the circle as well as to the hyperbola is
View SolutionThe circle x2+y2−8x=0 and hyperbola x29−y24=1 intersect at the points A and B. Then the equation of the circle with AB as its diameter is
View Solutionवृत्त x2+y2−8x=0 तथा अतिपरवलय x29−y24=1 एक-दूसरे को A तथा B बिन्दुओं पर प्रतिच्छेद करते हैं। धनात्मक प्रवणता वाली, वृत्त एवं अतिपरवलय की उभयनिष्ठ स्पर्श रेखा का समीकरण होगा : (i) 2x−√5y−20=0 (ii) 2x−√5y+4=0 (iii) 3x−4y+8=0 (iv) 4x−3y+4=0
View Solutionवृत्त x2+y2−8x=0 तथा अतिपरवलय x29−y24=1 एक-दूसरे को A तथा B बिन्दुओं पर प्रतिच्छेद करते हैं। AB को व्यास मानकर बनाये गये वृत्त का समीकरण होगा:
(i) x2+y2−12x+24=0 (ii) x2+y2+12x+24=0
(iii) x2+y2+24x−12=0 (iv) x2+y2−24x−12=0
View Solution
