The mean of the frequency distribution are 28 and 16 respectively. Find the median:
22.5
24
24.5
26
The correct Answer is:C
Topper's Solved these Questions
- STATISTICSBook:OSWAL PUBLICATIONChapter:STATISTICSExercise:Very Short Answer Type Questions
Explore 4 Videos
- STATISTICSBook:OSWAL PUBLICATIONChapter:STATISTICSExercise:Short Answer Type Questions
Explore 2 Videos
- STATISTICSBook:OSWAL PUBLICATIONChapter:STATISTICSExercise:BOARD CORNER (Long answer type questions)
Explore 7 Videos
- SOME APPLICATIONS OF TRIGONOMETRY (HEIGHTS AND DISTANCES) Book:OSWAL PUBLICATIONChapter:SOME APPLICATIONS OF TRIGONOMETRY (HEIGHTS AND DISTANCES) Exercise:CASE-BASED MCQs
Explore 15 Videos
- SURFACE AREAS AND VOLUMES Book:OSWAL PUBLICATIONChapter:SURFACE AREAS AND VOLUMES Exercise:BOARD CORNER (LONG ANSWER TYPE QUESTIONS)
Explore 9 Videos
Similar Questions
Knowledge Check
The mean and mode of a frequency distribution are 28 and 16 respectively .The median is
A22B23.5C24D24.5The median and mode of a frequency distribution are 26 and 29 respectively. Then , the mean is
A27.5B24.5C28.4D25.8If the mean and the mode of a moderately skewed frequency distribution are 90 and 96 respectively, then the median is
A93B92C98D88
In a frequency distribution mode is 7.88 , mean is 8.32 .find the median
View SolutionThe median of following frequency distribution is 24 years. Find the missing frequency x.
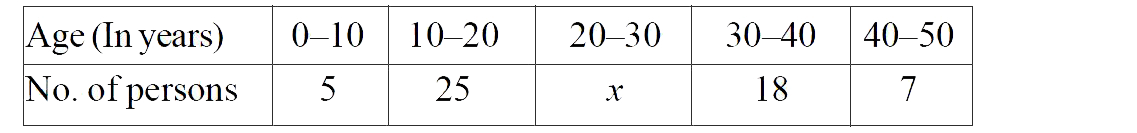
View SolutionIn the following question, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): If the median and mode of a frequency distribution are 150 and 154 respectively. Then its mean is 148.
Reason (R): Mean, median and mode of a frequency distribution are related as 3Mean=3Median - Mode.
View SolutionIf the median and mean of moderately asymmetrical frequency distribution are 72 and 74 respectively, then the mode is
View SolutionIf in a frequency distribution, the mean and median are 21 and 22 respectively, then its mode is approximately
View Solution
