The value of the integral 1∫0cot−1(1−x+x2)dx, is
The correct Answer is:xtan−1x−12log(1+x2)−(1+x2)−(1−x)tan−1(1−x)+12log{1+(1+x2)}+C
Step by step video solution for The value of the integral underset(0)overset(1)int cot^(-1) (1-x+x^(2))dx, is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- INDEFINITE INTEGRAL Book:ARIHANT MATHS ENGLISHChapter:INDEFINITE INTEGRAL Exercise:Exercise For Session 5
Explore 10 Videos
- INDEFINITE INTEGRAL Book:ARIHANT MATHS ENGLISHChapter:INDEFINITE INTEGRAL Exercise:Exercise For Session 6
Explore 10 Videos
- INDEFINITE INTEGRAL Book:ARIHANT MATHS ENGLISHChapter:INDEFINITE INTEGRAL Exercise:Exercise For Session 3
Explore 22 Videos
- HYPERBOLABook:ARIHANT MATHS ENGLISHChapter:HYPERBOLAExercise:Hyperbola Exercise 11 : Questions Asked in Previous 13 Years Exams
Explore 3 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBook:ARIHANT MATHS ENGLISHChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 8 Videos
Similar Questions
Evaluate the following Integrals :
∫x2(x−1)(x−2)(x−3)dx
View SolutionEvaluate the following Integrals :
∫x4−1x2(x4+x2+1)1/2dx
View SolutionEvaluate the following integrals
∫xdx9−16x4
View SolutionMatching the information given in the three columns of the following table column 1, 2 and 3 contain conics, equations of tangents in the conics and points of contact, respectively.
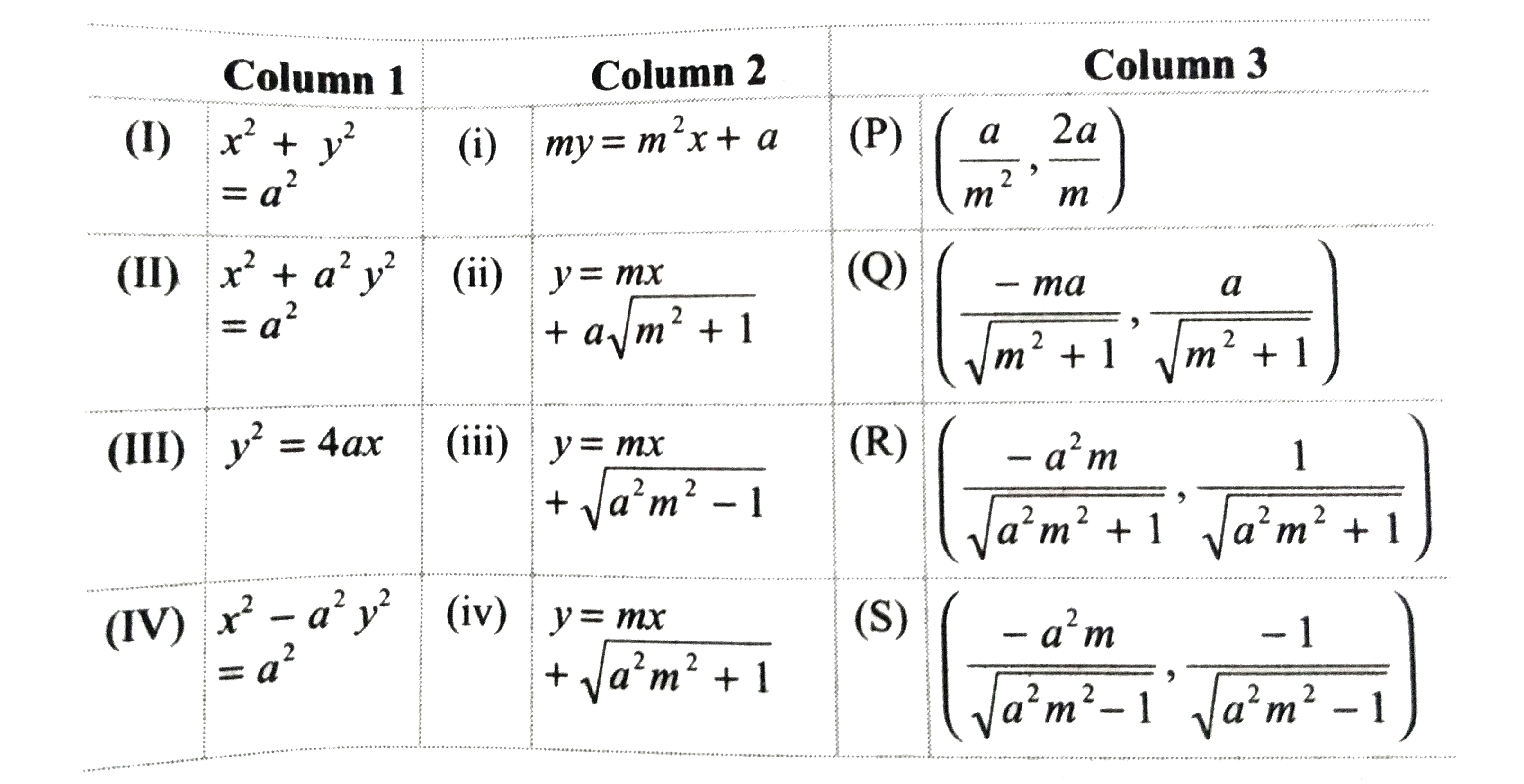
Q. The tangent to a suitable conic (column 1) at (√3,12) is found to be √3x+2y=4, then which of the following options is the correct combination?
View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
View Solutionसमाकलन ज्ञात कीजिए ।
1∫−1(x+1)dx
View Solutionसमाकलनों का मान प्रतिस्थापन का उपयोग करते हुए ज्ञात कीजिए।
1∫0xx2+1dx
View Solutionसमाकलन 1∫13(x−x3)13x4dx का मान है :
View Solutionसमाकलन 1∫1/3(x−x3)1/3x4dx का मान है
View Solution1∫0cot−1(1−x+x2)dx
View Solutionसमाकलन करें
1∫0√1−x1+xdx
View SolutionThe value of the integral 1∫01x2+2xcosα+1dx is equal to
View SolutionThe value of the integral
1∫1/3(x−x3)1/3x4dx is
View SolutionThe value of the integral 1∫0ex2dx lies in the integral
View SolutionChoose the correct answer
The value of the integral ∫113(x−x3)13x4dx is
View Solutionनिम्न निश्चित समाकलन का मान ज्ञात कीजिए।
1∫0x5√1+x21−x2 dx
View Solution
