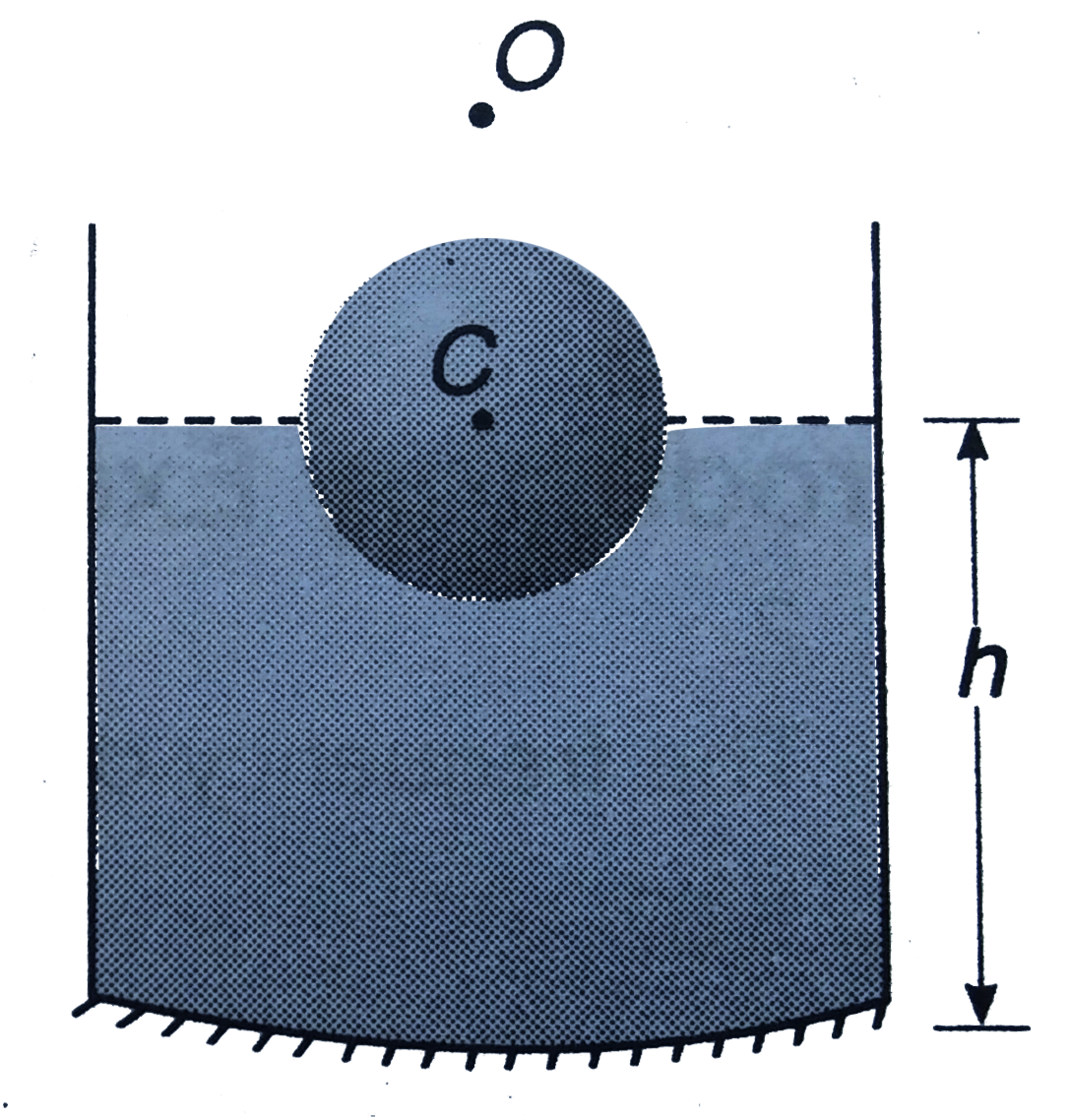
A transparent solid sphere of radius 2cm and density ρ floats in a transparent liquid of density 2ρ kept in a beaker. The bottom of the beaker is spherical in shape with radius of curvature 8cm and is silvered to make it concave mirror as shown in the figure. When an object is placed at a distance of 10cm directly above the centre of the sphere C, its final image coincides with it. Find h (as shown in the figure ), the height of the liquid surface in the beaker from the apex of the bottom. Consider the paraxial rays only. The refractive index of the sphere is 3/2 and that of the liquid is 4/3.
The correct Answer is:A, C
ViV=ρSρL=ρ2ρ=12
i.e. half the sphere is inside the liquid. For the
image to coincide with the object light should fall
normally on te sphere.
Using μ2v−μ1u=μ2−μ1R twice, we have
3/2v1−1−8=3/2−1+2
∴v1=12cm
Further, 4/3h−10−3/28=4/3−3/2−2
Solving this equation, we get
h=15cm
Topper's Solved these Questions
Similar Questions
Can the potential barrier across a p-n junction be measured by simply connecting a voltmeter across the junction ?
View SolutionA transparent solid sphere of radius 2 cm and density p floats in a transparent liquid of density 2 rho kept in a beaker. The bottom of the beaker is spherical in shape with its radius of curvature 8 cm and is silvered to make it a concave mirror as shown in Fig. When an object is placed a 10 cm directly above the centre of the sphere its final image coincide with it. If 'h' is the height of liquid surface from the apex of the bottom as shown in figure. Consider paraxial rays only for image formation. The refractive index of the sphere is 3/2 and that of the liquid is 4/3 .Answer the following questions. The image formed by transparent solid sphere (measured from the bottom point of the sphere) is nearly equal to
View SolutionA transparent solid sphere of radius 2 cm and density p floats in a transparent liquid of density 2 rho kept in a beaker. The bottom of the beaker is spherical in shape with its radius of curvature 8 cm and is silvered to make it a concave mirror as shown in Fig. When an object is placed a 10 cm directly above the centre of the sphere its final image coincide with it. If 'h' is the height of liquid surface from the apex of the bottom as shown in figure. Consider paraxial rays only for image formation. The refractive index of the sphere is 3/2 and that of the liquid is 4/3 .Answer the following questions. The value of h is (nearly equal to)
View Solutionकोई वस्तु अवतल दर्पण के सम्मुख 20 सेमी दूरी पर रखी है यदि दर्पण की वक्रता त्रिज्या 20 सेमी हो तो उसका प्रतिबिम्ब बनेगा
View SolutionA transparent solid sphere of radius 2 cm and density rho floats in a transparent liquid of density 2rho kept in a beaker. The bottom of the beaker is spherical in shape with radius of curvature 8 cm and is silvered to make it concave mirror as shown in the figure. When an object is placed at a distance of 10 cm directly above the centre of the sphere C, its final image coincides with it. Find h (as shown in the figure ), the height of the liquid surface in the beaker from the apex of the bottom. Consider the paraxial rays only. The refractive index of the sphere is 3//2 and that of the liquid is 4//3.
View SolutionFind the distance of the image, when an object is placed on the principal axis at a distance of 10 cm in front of a concave mirror whose radius of curvature is 8 cm.
View SolutionA linear object of heigth 10 cm is kept in front of concave mirror of radius of curvature 15 cm, at distance of 10 cm. The image formed is
View Solution10 সেমি ব্যাসার্ধবিশিষ্ট একটি নিরেট গোলক গলিয়ে একই ব্যাসার্ধবিশিষ্ট 8 টি গোলক তৈরি করা হলো।প্রত্যেকটি গোলকের বক্রতলের ক্ষেএফল কত?
View Solution
