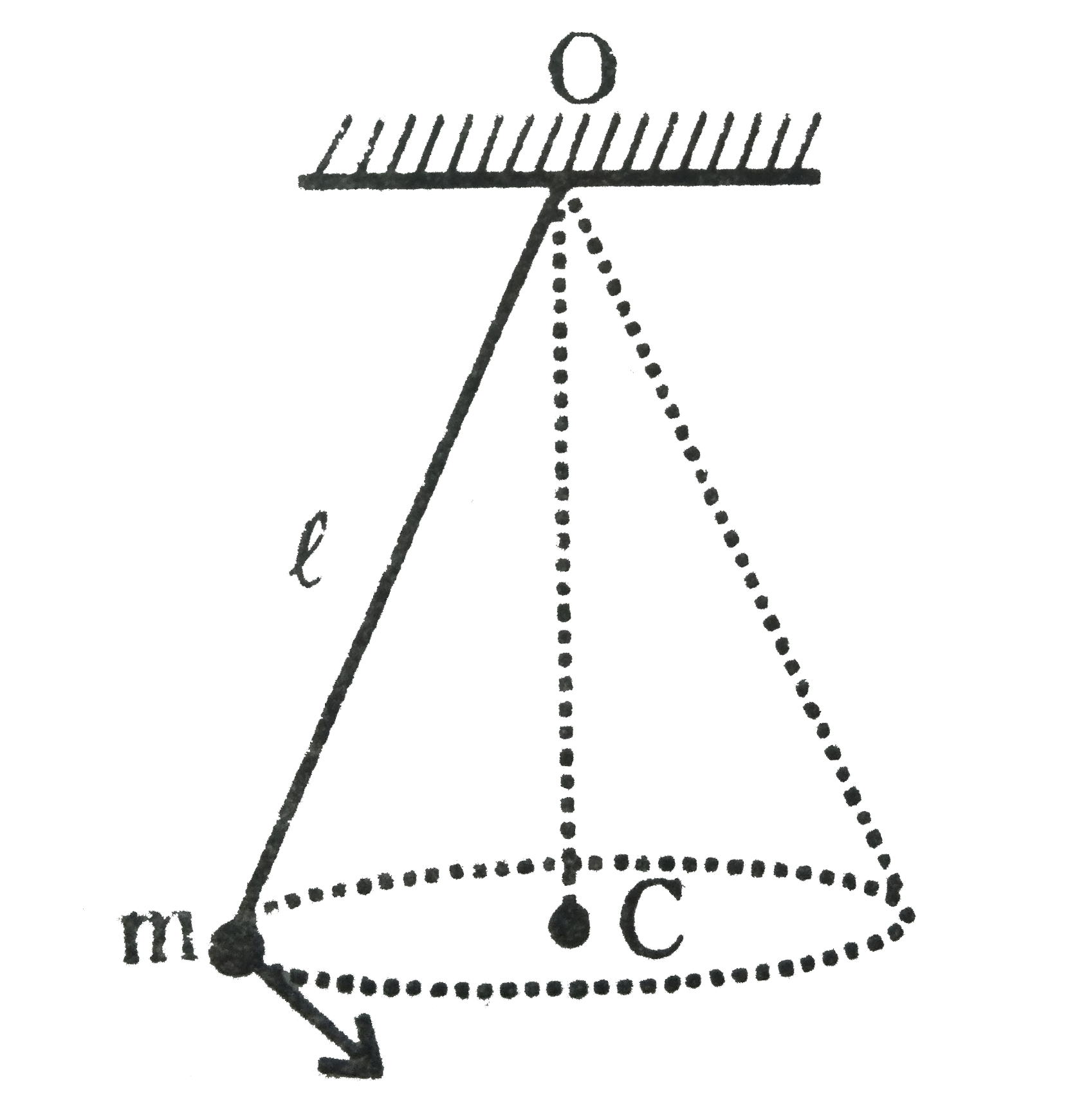
Three point masses are attached by light inextensible strings of various lengths to a point O on the ceiling. All of the masses swing round in horizontal circles of various radii with the same angular frequency ω (one such circle is drawn in the shown figure.) Then pick up the correct statement.
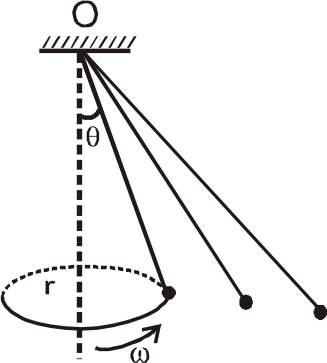
The vertical depth of each mass below point of suspension from ceilling is different.
The raduis of horizontal circular path of each mass is same.
All masses revolve in the same horizontal plane.
All the particles must have same mass.
For conical pendulum of length l , mass m moving along horizontal circle as shown
Tcosθ=mg.....(1)
Tsinθ=mω2lsinθ.......(2)
From equation (1) and equation (2) , lcosθ=gω2
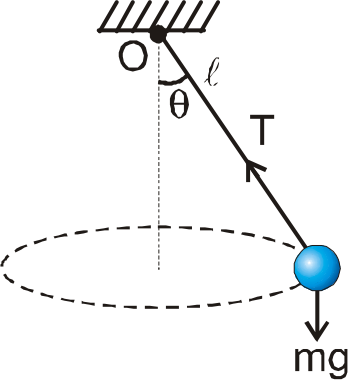
lcosθ is the vertical distance of bob below O point of suspension. hence if ω of all three pendulums are same, they shall revolve in same horizontal plane.
Alternate:
If we remember that time period T of conical pendulum is
T=2π√Lg where L is the vertical depth of bob below point of suspension. if T is same for three pendulums even L shall be also same. hence all three particles shall revolve in same horizontal plane.
Topper's Solved these Questions
Similar Questions
A particle of mass 21 g attached to a string of 70cm length Keeping the string always taut the ball describes a horizontal circle of radius 15cm Calculate the angular speed of the ball .
View SolutionThree balls each of mass 1 kg are attached with three strings each of length 1 m as shown in figure. They are rotated in a horizontal circle with angular velocity ω=4rad s−1 about point O. Match the following columns.
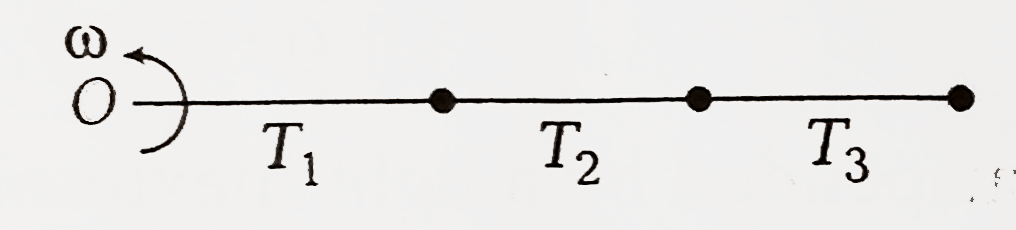
View Solution
Knowledge Check
Three masses of small size are attached by light inextensible strings of various lengths to a point O on the ceiling. All of the masses swing round in horizontal circles of various radii with the same angular frequency ω (one such circle is drawn in the shown figure.) Then pick up the correct statement.
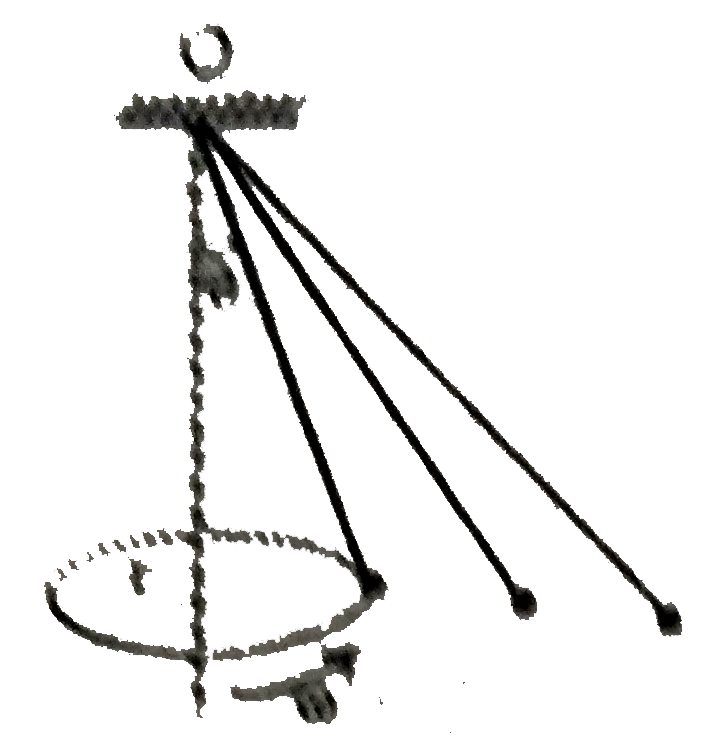 AThe vertical depth of each mass below point of suspension from ceilling is differentBthe radius of horizontal circular path of eachmass is sameCall masses revolve in the same horizontal planeDall the particles must have same mass.
AThe vertical depth of each mass below point of suspension from ceilling is differentBthe radius of horizontal circular path of eachmass is sameCall masses revolve in the same horizontal planeDall the particles must have same mass.A uniform chain of mass M and length L is rotated in a horizontal circle about its one end at an angular frequency ω. The tension at its axis is
AMω2LBMω2L8CMω2L4DMω2L2
Two spheres of equal masses are attached to a string of length 2 m as shown in figure. The string and the spheres are then whirled in a horizontal circle about O at a constant rate. What is the value of the ratio:A12B23C32D2
A bob of mass m attached to an inextensible string of length l, is suspended from a vertical support. Bob rotates in a horizontal circle with angular speed ω and string makes an angle of θ with the vertical. Find the angular momentum of bob about axis of rotation
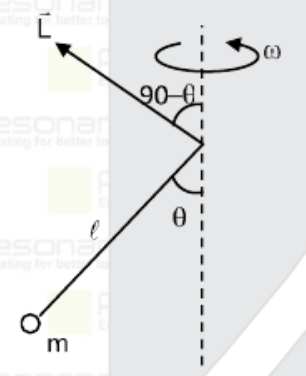
View SolutionA bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
View SolutionA small ball of mass m suspended from the celling at a point O by a thread of length l moves along a horizontal circle with a constant angular velocity ω.
 .
.
View SolutionA particle is attached by a light string of length 3 a to a fixed point and describes a horizontal circle of radius a with uniform angular velocity ω If, when the particle is moving in this manner, is suddenly stopped and then let go,find its velocity when the string is vertical in its subsequent motion :
View SolutionA paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are

View Solution

