A plane light wave with wavelength λ=0.60μm falls normally on a sufficiently large glass plate having a round recess on the oppiste side (Fig.) For the observation point P that recess correcponds to the first one and and a half Fresnel zones. Find the depth h of the recess at which the intensity of light at the point P is
(a) maximum,
(b) minimum,
(c ) equal to the intensity of incident light.
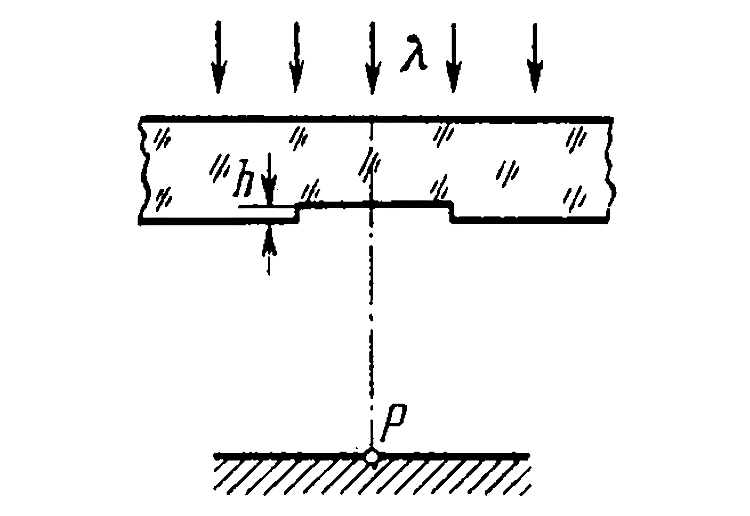
We could require the comtribution to the amplitude of a wave at a point from half a Fresnel zone. For this we proceed directly from the Fresnel Huyghens principle. The complex amplitude is written as
E=∫K(φ)a0re−ikrdS
Here K(φ) is a factor which depends on the angle φ between a normal →n to the area dS and the direction from dS to the point P and r is the distance from the element dS to P.
We see that for the first Fresnal zone

(using r=b+ρ22b (for √ρ2b2))
E=a0b∫√bλ0e−ikb−ikρ2/2b2πρdρ(K(φ)≈1)
For the first Fresnel zone r=b+λ/2 so r2=b2+bλρ and ρ2=bλ
Thus E=a0be−ikb2π∫bλ20e−kxbdx
=a0b2πeikbeikλ/2−1−ik/b
=a0k2πie−ikb(−2)=−4πkia0e−ikb=A1
For the next half
E=a0be−ikb2π∫3bλ4bλ2e−ikx/bd×
=a0k2πie−ikb(e−i3kλ4−e−ikλ/2)
=a0k2πie−ikb(+1+i)=−A1(1+i)2
If we calaclate the contribution of the full 2nd Fresnel zone we will get −A1. If we take account of the factors K(φ) and 1r which decrease monotonically we expect the contribution to change to −A2. Thus we write for the combtribution of the half zones in the 2nd Fresnel zone as
−A2(1+i)2 and −A2(1−i)2
The part lying in the recess has an extra phase difference equal to −∂=−2πλ(n−1)h. Thus the full amplitude is (note that the correct from is e−ikr)
(A1−A22(1+i))e+l−A22(1−i)+A3−A4+........
≈(A12(1−i))e+l−A22(1−i)+A32
≈(A12(1−i))e+i∂+iA12 (as A2≈A3≈A1) and A3−A4+A5......=A32.
The corresponding intensity is
I=A214[(1−i)e+i∂+ie][(1+i)e−i∂−i]
I0[3−2cos∂+2sin∂]=I0[3×2√2sin(∂−π4)]
(a) For maximum intensity sin(∂−π4)=+1
or ∂−π2=2kπ+π2,k=0,1,2,....
∂=2kπ+3π4=2πλ(n−1)h
so h=λn−1(k+38)
(b) For minimum intensity
sin(δ−π4)=1
∂−π4=2kπ+3π2 or ∂=2kπ+7π4
so h=λn−1(k+7π8)
(c ) ForI=I0cosδ=0sinδ=−1} or {sinδ=0cosδ=+1
Thus δ=2kπ+3π2h=kλn−1
or δ=2kπ+3π2,hλn−1(k+3π4)
Similar Questions
A plane monochromatic light wave falls normally on an opaque half-plane. A screen is located at a distance b = 100 cm behind the half-plane. Making use of the cornu spiral (Fig.) find : (a) the ratio of intensities of the first maximum and the neighbouring minimum, (b) the wavelength of light if the first two maxima are separated by a distance Deltax = 0.63mm .
View SolutionA plane light wave with wavelength lambda = 0.65 mum falls normally on a large glass plate whose opposite side has a longrectangular recess 0.60mm wide. Using Fig. find the depth H of the recess at which the diffraction pattern on the screen 77 cm away from the plate has the maximum illuminance at its centre.
View SolutionA plane light wave with wavelength lambda = 0.65mum falls normally on a large glass plate whose opposite side has a large and an opaque strip of width a = 0.30mm (Fig.) A screen is placed at a distance b = 110 cm from the plate. The height h of the ledge is such that the intensity of light at point 2 of the screen is the heighest possible. making use of Fig. find the ratio of intensities at point 1 and 2 .
View SolutionA plane monochromatic light wave of intensity I_(0) falls normally on an opaque screen with a long slit having a semicircular cut on one side (Fig.) The edge of the cut coincides with the boundary line of the first Fresnel zone for the observation point P . Thw width of the slit measure 0.90 of the radius of the cut. using Fig. find the intensity of light at the point P .
View SolutionA plane monochromatic light wave falls normally on an opaque screen shaped as a long strip with a round hole in the middle. For the observation point P the hole corresponds to half the Fresnel zone, with the hole diameter being eta = 1.07 times less then the width of the strip. Using Fig. find the intensity of light at the point P provided that the intensity of the incident light is equal to I_(0) .
View SolutionA plane light wave with wavelength λ falls normally on a phase diffraction grating whose side view is shown in Fig. The grating is cut on a glass plate with refractive index n. Find the depth h of the lines at which the intensity of the central Fraunhofer maximum is equal to zero. what is in this case the diffraction angle corresponding to the first maximum?
View SolutionA plane monochromatic wave of natural light with intensity I0 falls normally on an opaque screen with round hole corresponding to the first Fresnel zone for the observation point P. Find the intensity of light at the point P after the hole was converd with two identical Polaroids whose principle directions are mutually perpendicular and the boundary beween them passes
(a) along the diameter of the hole,
(b) along the circumference of the circle limiting the first half of the fresnel zone.
View SolutionPlane monochromatic light with intensity I_(0) falls normally on an opaque disc closing the first Fresnel zone for a point on the screen in front of the wave front. What would be the intensity I at the same point if (a) half of the disc along the diameter were removed, (b) half of the external half is removed along the the diameter ?
View Solution

