A plane monochromatic light wave of intensity I0 falls normally on an opaque screen with a long slit having a semicircular cut on one side (Fig.) The edge of the cut coincides with the boundary line of the first Fresnel zone for the observation point P. Thw width of the slit measure 0.90 of the radius of the cut. using Fig. find the intensity of light at the point P.
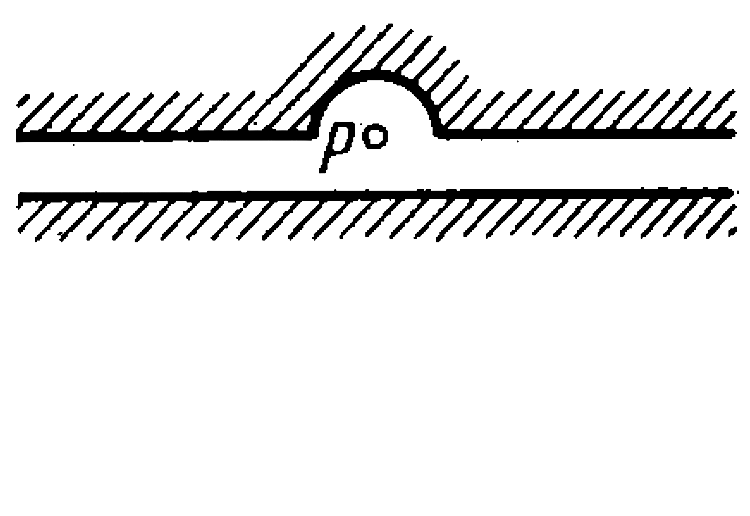

we apply the formula of problem 5.103 and calculate
∫aperturea0re−ikrdS=∫semicircle+∫slit
The contribution of the full 1st Fresnel zone has been evaluated in 5.103. The contribution the semi-circule is one half of it and is
−2πkia0e−ikb=−ia0λe−ikb
The contribution of the slit is
a0b0.90√bλ∫0e−ikbe−ikx22bdx∞∫−∞e−iky2/2bdy
Now ∞∫−∞e−iky2/2bdy=∞∫−∞e−iπy2bλdy
√bλ2∞∫−∞e−iπy2/2du=√bλe−iπ/4
Thus the contribution of the slit is
a0b√bλe−ikb−iπ/40.9×√2∫−∞e−iπu2/2du√bλ2
=a0λe−ikb−iπ/41√21.27∫0e−iπu2/2du
Thus the intensity at the observation point P on the screen is
a20λ2∣∣∣−i+1−i2(C(1.27)−iS(1.27))∣∣∣2=a20λ2∣∣∣−i+(1−i)(0.67−0.65i)2∣∣∣2
(on using (C(1.27)=0.67 and S(1.27)=0.65)
=a20λ2|−i+0.01−0.66i|2
a20λ2|0.01−1.66i|2
=2.76a20λ2
Now a20λ2 is the intensity due to half of 1st Fresnel zone and is therefore equal to I0. (It can also be obtained by doing the x-intergal over −∞ to +∞).
Thus I=2.76I0.
Similar Questions
A plane monochromatic light wave falls normally on an opaque screen with a long slit whose shape is shown in Fig. Making use of Fig. find the ratio of intensities of light at points 1,2 and 3 located behind the screen at equal distances from it. For point 3 the rounded-off edge of the slit coincides with the boundary line of the first Fresnel zone.

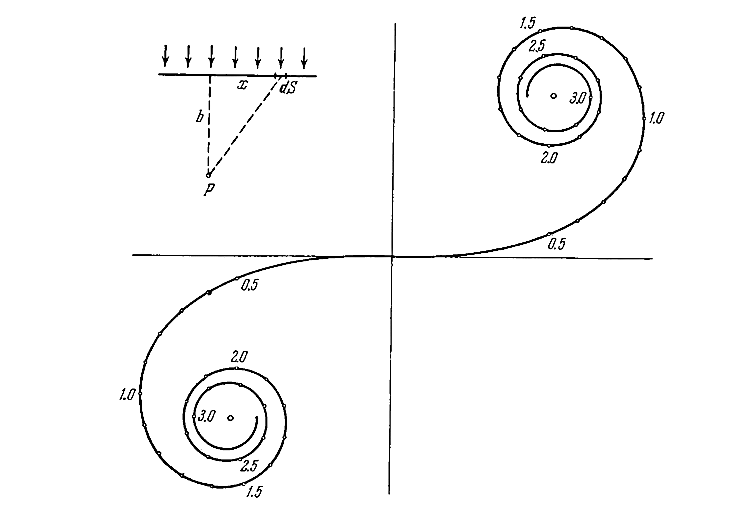
View SolutionA plane monochromatic light wave falls normally on an opaque screen shaped as a long strip with a round hole in the middle. For the observation point P the hole corresponds to half the Fresnel zone, with the hole diameter being eta = 1.07 times less then the width of the strip. Using Fig. find the intensity of light at the point P provided that the intensity of the incident light is equal to I_(0) .
View SolutionA plane monochromatic wave of natural light with intensity I0 falls normally on an opaque screen with round hole corresponding to the first Fresnel zone for the observation point P. Find the intensity of light at the point P after the hole was converd with two identical Polaroids whose principle directions are mutually perpendicular and the boundary beween them passes
(a) along the diameter of the hole,
(b) along the circumference of the circle limiting the first half of the fresnel zone.
View SolutionIn a Young's double-slit experiment using identical slits, when one slit is used, the total energy reaching the screen is E_(0) and the intensity of light at any point on the screen is I_(0) . When both slits are usedm and fringes are formed on the screen, the total energy reaching the screen is E and the maximum intensity on the screen is I. Then,
View SolutionPlane monochromatic light with intensity I_(0) falls normally on an opaque disc closing the first Fresnel zone for a point on the screen in front of the wave front. What would be the intensity I at the same point if (a) half of the disc along the diameter were removed, (b) half of the external half is removed along the the diameter ?
View SolutionA plane monochromatic light wave of intensity I_(0) falls normally on the surfaces of the opaque screens which are shaped as shown in the figure here. The shaped as shown in the gigure here. The rounded-off edge coinicides with the boundary of the first Fresnel zone. Find the intensity of the screens at a point located behind the point P.
View SolutionIn Young's double-slit experiment, the intensity of light in front of one of the slits on a screen is I0/2 where I0 is the maximum intensity. The distance between the slits is 5λ where λ is the wavelength of monochromatic light. How far away is the screen from the slit?
View SolutionA Young's double slit experiment uses a monochromatic light of wavelength lambda . The intensity of each slit is same and is equal to I_(0) . What will be the resultant intensity at a point where waves interfere at a path difference of (lambda)/2 ?
View Solution

