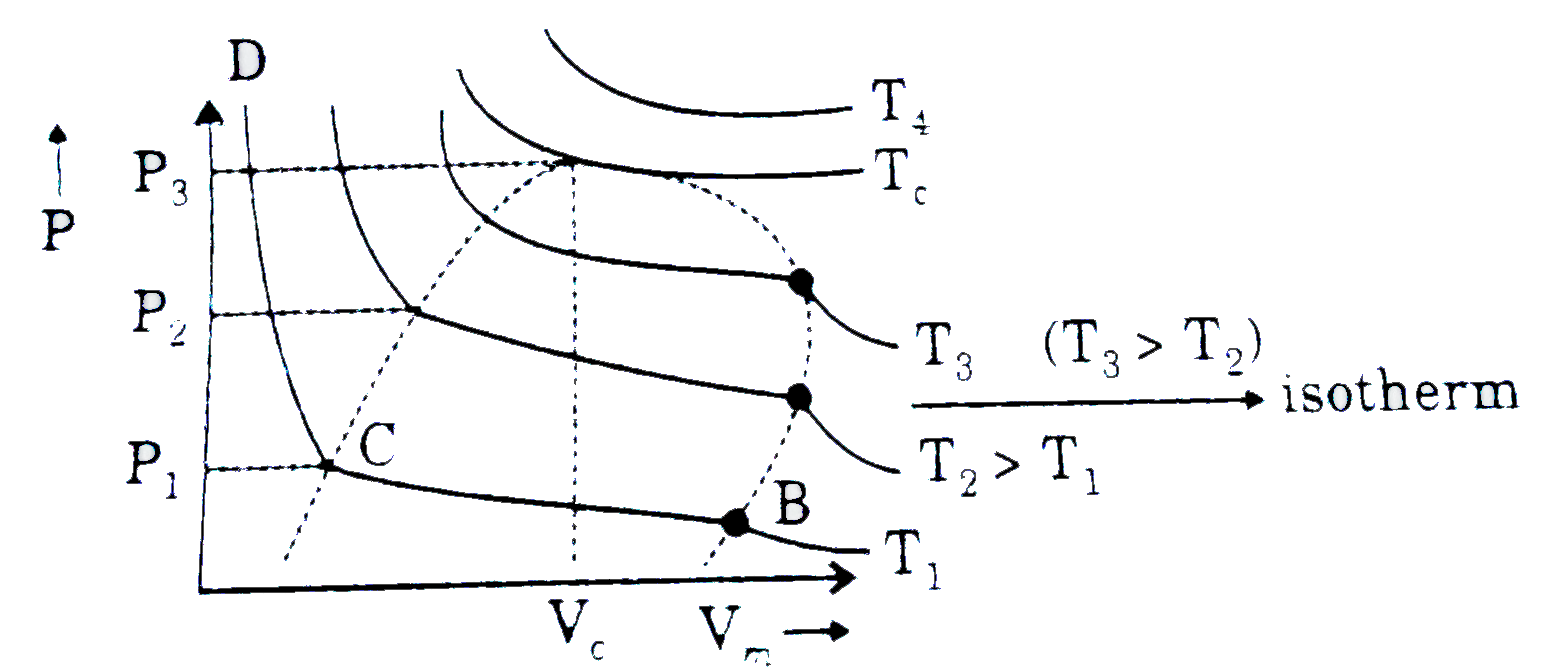
When perssure is increase at constant temperature, volume of gas decreases, AB → gases,Bc → vapour + liquid ,CD →liquid critical point .At this all the physical properties of liquid phase as density of liquid = density if vapour.
Te or critical temp : Temperature above which a gas can not be liquified
Ve or critical volume : Volume occupied by one mole of gas at Te abd Pe.
Critical constant Using van der Waals' Equations
(P+aV2m)(Vm−b)=RT
⇒(PV2m+a)(Vm−b)=RTV2m
PV3m+aVm−PbV2m=ab−RTV2m=0
⇒V3m−V2m(b+RTeP)+apVm−abp=0
Since equation is cubic in Vm hence there will be roots of equation at any temperature and pressure.At critical point van der Waals' equation will be
V3m−V2m(b+RTcPc)+apcVm−abpc=0 ....(i)
But at critical point all three roots of the equation should be equal, hence equation should be :
Vm=Vc
(Vm−Vc)3=0
Vm−3V2mVc+3VmV2c−V3c=0....(ii)
Comparing with equation (i)
b+RTcpc=3Vc ...(iii)
apc=3V2e...(iv)
abpc=V3c....(v)
from eqns.(iv) and (v0, Vc=3b
from eq. (iv) pc=a3V2c substituting pc=a3(3b)2=a27b2
from e.q (iii) RTcpc=3Vc−b=9b−b=8b
⇒Tc=8a27Rb
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slpoe will be negative zero is the maximum value of slope
(∂P∂Vm)Tc=0...(iv)
∂∂Vm(∂P∂Vm)Tc=0
[Mathematically such points are known as point of inflection (where first two derivatives becomes zero) Using the two TcPc and Vc can be calculated
If the critical constants for a hypothetical van der Waals' gas are Vc=150cm2mol−1,pc=300K Then the approxomate radius of the molecule is :
(TakeR=112Latmmol−1K−1]
(752πNA)1/3
(758πNA)1/3
(3πNA)1/3
(3256πNA)1/3
The correct Answer is:B
Similar Questions
Assertion. At the critical temperature, the densities of the gaseous and liquid phase become equal. Reason. At the critical point, surface of separation between the liquid phase and the gaseous phase disappears.
View SolutionAssertion. Menscus of a liquid disappears at critical temperature. Reason. Density of a liquid and its gaseous phase become equal at the critical temperature.
View SolutionWhat happens when a liquid a heated to the critical temperature of its vapour?
View SolutionThe vapour pressure of water at 20∘C is 17.54mm Hg. then the vapour pressure of the water in the apparatus shown after the piston is lowered, decreasing the volume of the gas above the liquid to one half of its initial volume (temp. constant) is
View SolutionAssertion (A) At critical temperature liquid passes into gaseous state imperceptibly and continuously.
Reason (R) The density of liquid and gaseous phase is equal to critical temperature.
View SolutionExplain relation between Fluid State, Liquid - Gas State, Critical temperature and Vapour form of substances.
View SolutionAssertion (A) : At critical temperature liquid passes into gaseous state imperceptibly and continuously.
Reason (R ) : The density of liquid and gaseous phase is equal to critical temperature.
View SolutionA sample of gas has a volume of V_(1) litre at temperature t_(1).^(@)C . When the temperature of the gas is changed to t_(2).^(@)C at constant pressure, then the volume of the gas was found to increase by 10%. The percentage increase in temperature is
View Solution

