P is any point on AD, the median of ΔABC. Prove that ΔABP=ΔACP.Solution in Bengali
Step by step video & image solution for P is any point on AD, the median of DeltaABC. Prove that DeltaABP=DeltaACP. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
If E be the mid-point of the median AD of ΔABC, then prove that ΔBED=14ΔABC.
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
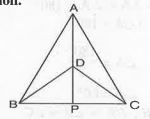 ).If AD is extended to intersect BC at P, show that ΔABP≅ΔACP.
).If AD is extended to intersect BC at P, show that ΔABP≅ΔACP.
View SolutionIn a ΔABC median AD is produced to X such that AD = DX. Prove that ABXC is a parallelogram.
View Solutionसिद्ध करें कि ΔABC एक समद्विबाहु त्रिभुज है यदि माध्यिका AD, BC पर लम्ब है।
View SolutionDeltaABC Of angleA The bisector of AD is AD, P is any single point on AD Prove that the lengths inserted from AB to AC and AC from P are equal.
View Solutionकिसी ΔABC में माध्यिका AD को P तक इस प्रकार बढ़ाया जाता है किAD=DP । सिद्ध कीजिए कि ABPC एक समांतर चतुर्भुज है।
View SolutionIn the given figure, AD is median of ΔABC and E is any point on median AD. Prove that Area (ΔABE) = Area (ΔACE)
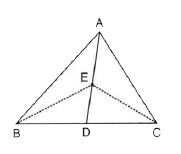
View SolutionA(4,3),B(6,5)andC(5,−2) are the vertices of a ΔABC, if P is a point on BC such that BP:PC=2:3. Find the co-ordinates of P and then prove then ar (ΔABP):ar(ΔACP)=2:3.
View Solution