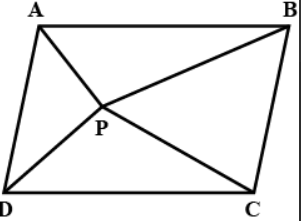
In Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)
Given ABCD is a parallelogram. So, AB||CD,AD||BC.
(i) Now, draw MPR parallel to AB and CD both and also draw a perpendicular PS on AB.
.:MR||ABandAM||BR
∴ABRM is a parallelogram
∴Ar(∣∣gmABRM)=AB×PS...(1)
and ar(ΔAPB)=12×AB×PS
⇒ar(ΔAPB)=12ar(∣∣gmABRM) [from (1)]
Similarly, ar(ΔPCD)=12ar(∣∣gmMRCD)
Now, ar(ΔAPB)+ar(ΔPCD)=12ar(∣∣gmABRM)+12ar(∣∣gmMRCD)
=12ar(∣∣gmABCD)...(2)
(ii) Similarly, we can draw a line through P parallel to AD and through the point P draw perpendicular on AD, we can prove that
ar(ΔAPD)+ar(ΔPBC)=12ar(∣∣gmABCD)
From (2) and (3), we get
ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)

Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise
34 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )
5 Videos
Similar Questions
The base of a parallelogram is 3 times of its corresponding height. If the area of the parallelogram is 48cm2, then find the base and the corresponding height of the parallelogram.
View SolutionThe lengths of the diagonals of a rhombus are 12 cm and 16 cm. Find the area of rhombus
View SolutionIn Δ ABC, D is the mid-point of AB and P is any point on BC. If CQ∣∣PD meets AB and Q (shown in figure), then prove that
ar(ΔBPQ)=12ar(ΔABC).

View SolutionAB and CD are two chords of a circle such that AB=6 cm, CD=12 cm and ABCD. If the distance between AB and CD is 3 cm, find the radius of the circle.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show thatar (APB) × ar (CPD) = ar (APD) × ar (BPC).
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A parallel to CP meets CB produced in Q and the parallelogram PBQR completed. Show that ar(^(gm)ABCD)=ar(^(gm)BPRQ). CONSTRUCTION : Join AC and PQ. TO PROVE : ar(^(gm)ABCD)=ar(^(gm)BPRQ)
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
View SolutionIf p^(a)=q^(b)=r^(c)=s^(d) and p,q,r,s are in G.P then a,b,c,d are in
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)

View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each at P. Show That: ar(APB)×ar(CPD)=ar(APD)×ar(PBC)
View SolutionABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that: ar (ADO)=AR (CDO) ar ( ABP)= ar ( CBP)
View SolutionIn A ABC , P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar(PRQ)=12ar(ARC)
View SolutionIf AD is median of ABC and P is a point on AC such that ar (ADP): ar (ABD)=2:3, then ar(PDC):ar (ABC) is 1:5 (b) 1:5 (c) 1:6 (d) 3:5
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) × ar (CPD) = ar (APD) × ar (BPC).
View Solution
