A monoatomic gas follow a process TV= constant. Calculate the ratio of work done to change in internal energy when the gas goes form one state to another.
A
23
B
−23
C
53
D
75
Text Solution
The correct Answer is:B
ΔU=nRΔT(γ−1)
ΔW=nRΔT(1−η) Where η is a constt.
ΔWΔU=nRΔT/(1−η)nRΔT/(γ−1)
=−2/3 where γ=5/3
η=2
|
Similar Questions
Knowledge Check
Change in internal energy in an isothermal process for ideal gas is
AZeroB(+) veC(-) veDCannot be predictedIn an adiabatic process 90 J of work is done on the gas. The change in internal energy of the gas is
A−90jB+90jC0 jDDepends on initial temperatureCalculate the work done by the gas in the state diagram shown.
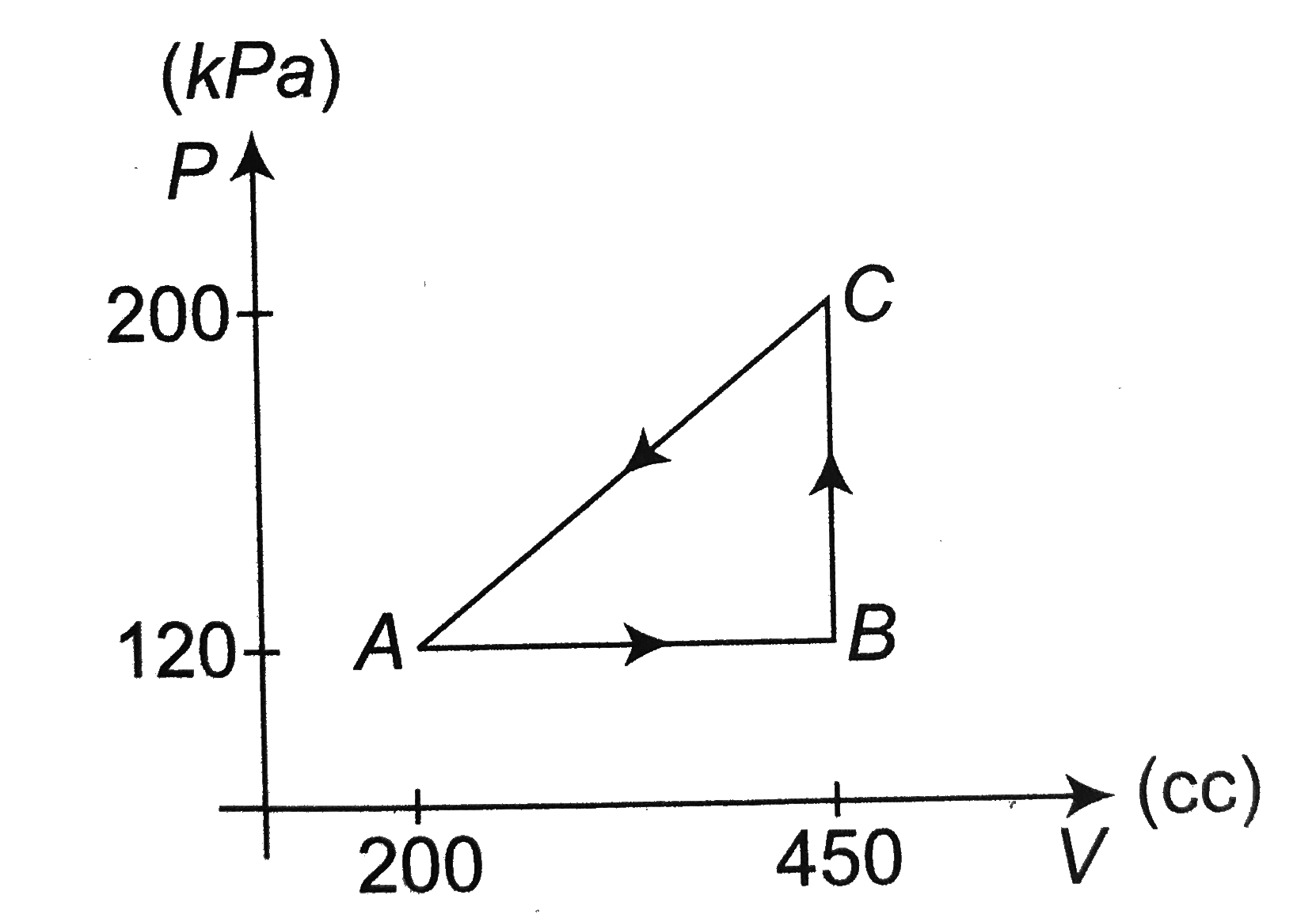 A30JB20JC−20JD−10J
A30JB20JC−20JD−10J
[H_(2)" gas undergoes process where "PV^(2)=" constant.The ratio of work done by gas to modulus of change in "],[" its internal energy as the gas expands is "(2)/(N).N" is equal to "]
View SolutionV-T graph of a process of monoatomic ideal gas is shown in figure.
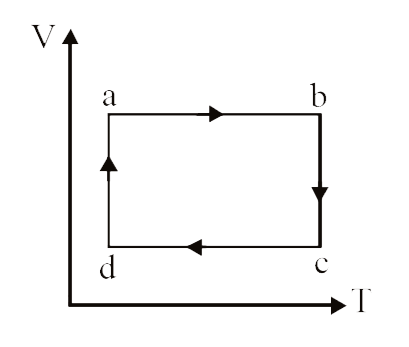
Change in internal energy of the gas is zero in process(s)-
View SolutionWhen an ideal monoatomic gas is heated at constant pressure,the fraction of heat energy supplied which increases internal energy of the gas is ?
View SolutionIn an isothermal expansion change in internal energy and work done by the gas are respectively
View SolutionIn an isothermal expansion change in internal energy and work done by the gas are respectively
View Solution


