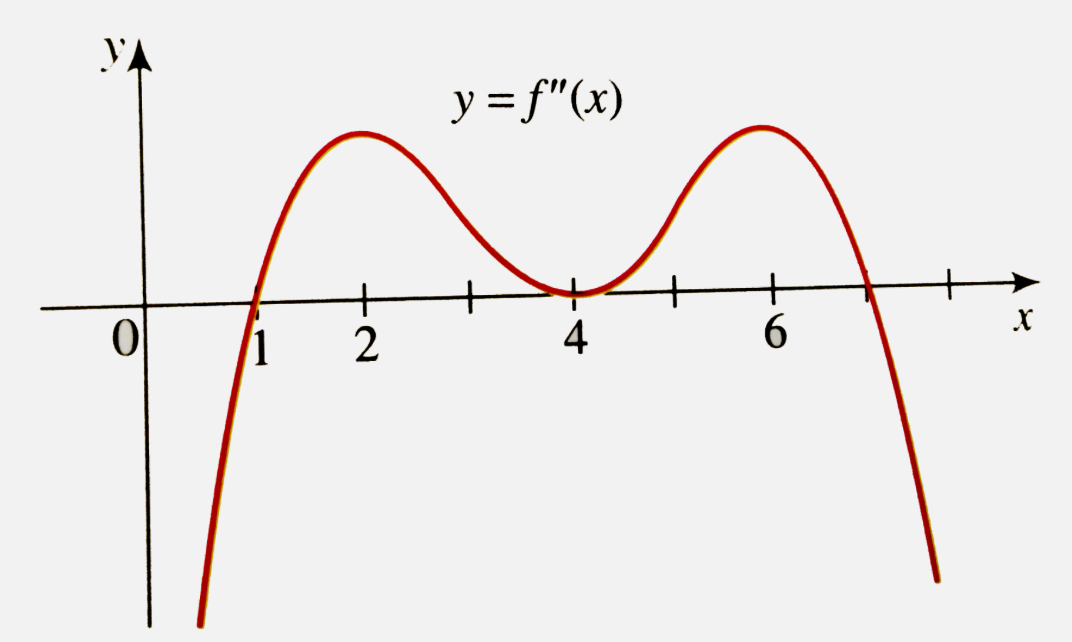
The graph of the second derivation f''(x) is given in the following figure. State the x - coordinate of the point of inflection of f. Given reasons for your answer.
(##CEN_GRA_C01_S01_024_Q01.png" width="80%">
x = 1 is the point of inflection as f'' changes sign from '-' to '+' with f''(1) = 0.
So the concavity of the curve changes from downward to upward.
x = 7 is the point of inflection as f'' changes sign from '+' to '-' with f''(7) = 0. So the concavity of curve changes from upward to downward.
At x = 4, f'' = 0, but f'' does not change sign. So x = 4 is not a point of inflection.
Topper's Solved these Questions
- GETTING STARTED WITH GRAPHSBook:CENGAGEChapter:GETTING STARTED WITH GRAPHSExercise:Exercise
Explore 18 Videos
- FUNCTIONSBook:CENGAGEChapter:FUNCTIONSExercise:Question Bank
Explore 30 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBook:CENGAGEChapter:GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSExercise:Exercise
Explore 18 Videos
Similar Questions
Does the following graph pass the vertical or horizontal line test ?

View SolutionIf f(x)=2x−1 then number of solution (s) of the equation |f(x)|=|f(|x|−1)| is (are)
View SolutionDraw the graph of y=tan−1x+cot−1x
View SolutionFor a particle moving along the x-axis, x-t graph is as given as graph in figure. Mar the correct statement (s). (#BMS_V01_MAA_E01_052_Q01.png" width="80%">
View SolutionFollowing is the graph of y = f(x).
(##CENGRAC01S01005_Q01.png width=80%><br>F∈dthes√oftheequation f(x) = 0, f(x) = 4 and f(x) = 10.
View SolutionThe graph of y = f(x) is shown, find the number of solution of f(f(x)) = 2.
(##CEN_GRA_C01_S01_007_Q01.png" width="80%">
View SolutionThe graph of y=f(x) is as shown in the following figure.
(##CEN_GRA_C01_S01_016_Q01.png" width="80%">
Identify the points of discontinuity and give the reason for the same.
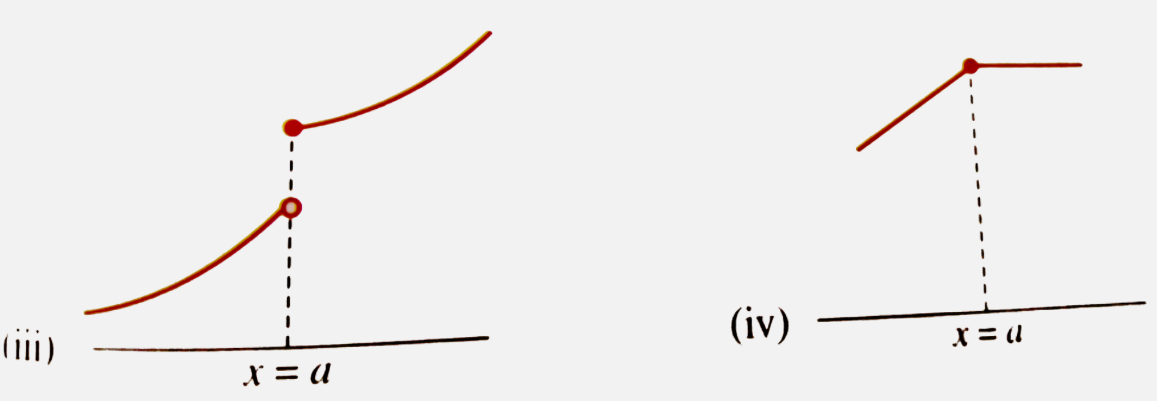
View SolutionFor each of the following graphs, comment whether f(x) is increasing or decreasing or neither increasing nor decreasing at x = a.
(##CEN_GRA_C01_S01_018_Q01.png" width="80%">
View SolutionThe diagram shows the graph of the derivative of a functin f(x) for 0≤x≤4 with f(0) = 0. Which of the following could be correct statements for y = f(x)?
(##CENGRAC01S01021_Q01.png width=80%><br>(a)Tan≥ntl∈e→y=f(x)atx=0makesan∠of sec^(-1) sqrt 5 with the x - axis.
(b) f is increasing in (0, 3).
(c) x = 1 is both an inflection point and the point of local extremum.
(d) Number of critical point on y = f(x) is two.
View SolutionThe graph of the derivative f'(x) is given in the following figure.
(b) Find the values of x for which f has local maximum or minimum.
(c) Find the intervals in which f is concave upward or downward.
(d) Find the point of inflection.
(##CEN_GRA_C01_S01_023_Q01.png" width="80%">
View SolutionThe figure shows the graphs of f, f' and f'' . Identify each curve and explain your choices.
(##CEN_GRA_C01_S01_025_Q01.png" width="80%">
View SolutionIf x0 is the x - coordinate of the point of inflection of a curve y=f(x) then (second derivative exists) ………….. .
View SolutionIn the given (##AKS_TRG_AO_CHE_XII_V02_B_C03_E02_024_Q01.png" width="80%"> , overet(PhMgBr )to (X) , X will be
View SolutionThe graph of the second derivation f''(x) is given in the following figure. State the x - coordinate of the point of inflection of f. Given reasons for your answer.
View SolutionAnalyse the figure and match the columns given below. ( ## EXP_SPS_PHY_XII_C04_E05_022_Q01 .png" width="80%">
View Solution

