In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ. Show that:
(i) ΔAPD≅ΔCQB
(ii) AP=CQ
(iii) ΔABC
(iv) AQ=CP
(v) APCQ is a parallelogram.

i) In ΔAPD and ΔCQB,
=>AD = CB (Opposite sides)
=>∠ADP = ∠CBQ (Alternate interior angles)
=> DP = BQ (Given)
So,ΔAPD ≅ ΔCQB (by SAS congruence rule)
(ii) Since ΔAPD ≅ ΔCQB,
∴ AP = CQ
(iii) In ΔAQB and ΔCPD,
=>∠ABQ = ∠CDP (Alternate interior angles )
=>BQ = DP (known)
=>AB = CD (Opposite sides )
∴ ΔAQB ≅ ΔCPD (Using SAS congruence rule)
(iv) Since ΔAQB ≅ ΔCPD,
∴ AQ = CP
(v) Using (ii) and (iv)
AQ = CP and AP = CQ
Since opposite sides in quadrilateral APCQ
are equal to each other, thus APCQ is a parallelogram.
Similar Questions
In parallelogram ABCD two points P and Q are taken on diagonal BD such that DP = BQ (set figure). Show that:
(i)ΔAPD≅CQB(ii)AP=CQ(iii)ΔAQB≅ΔCPD(iv)AQ=CP(v)APCQis a parallelogram. ltbegt
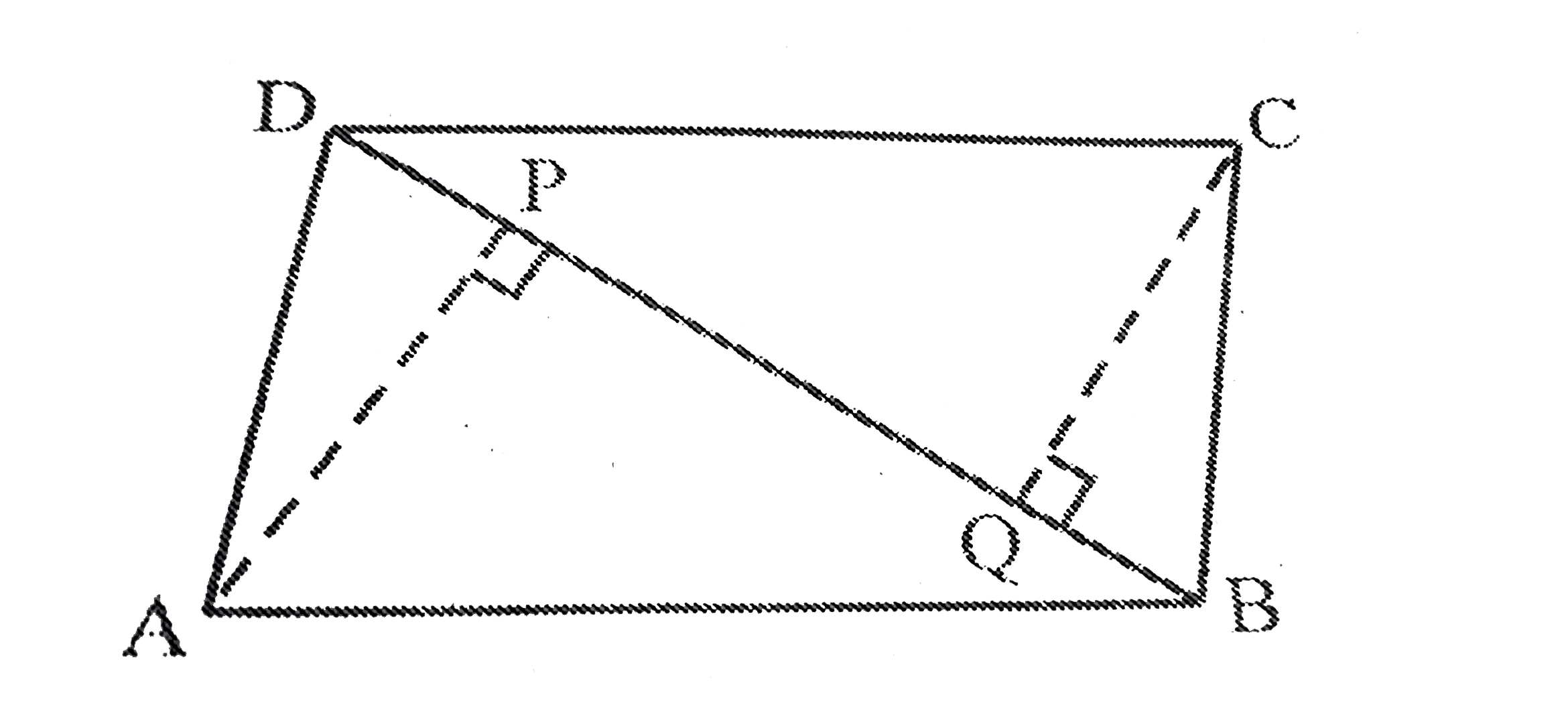
View SolutionABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD . Show that
(i) ΔAPB≅ ΔCQD
(ii) AP = CQ
View Solution
Knowledge Check
ABCD is a parallelogram. P and Q are mid points of BC & CD. Find the area of ΔAPQ if area of ΔABC is 12.
AtrapeziumBparallelogramCsquareDnone of these
In a parallelogram ABCD, points P and Q are points of trisection of diagonal BD. Prove that CQ is parallel to AP.
View SolutionIn Figure, two chords AB and CD intersect each other at the point P. Prove that:
(i) ΔAPC~ΔDPB
(ii) AP⋅PB=CP⋅DP

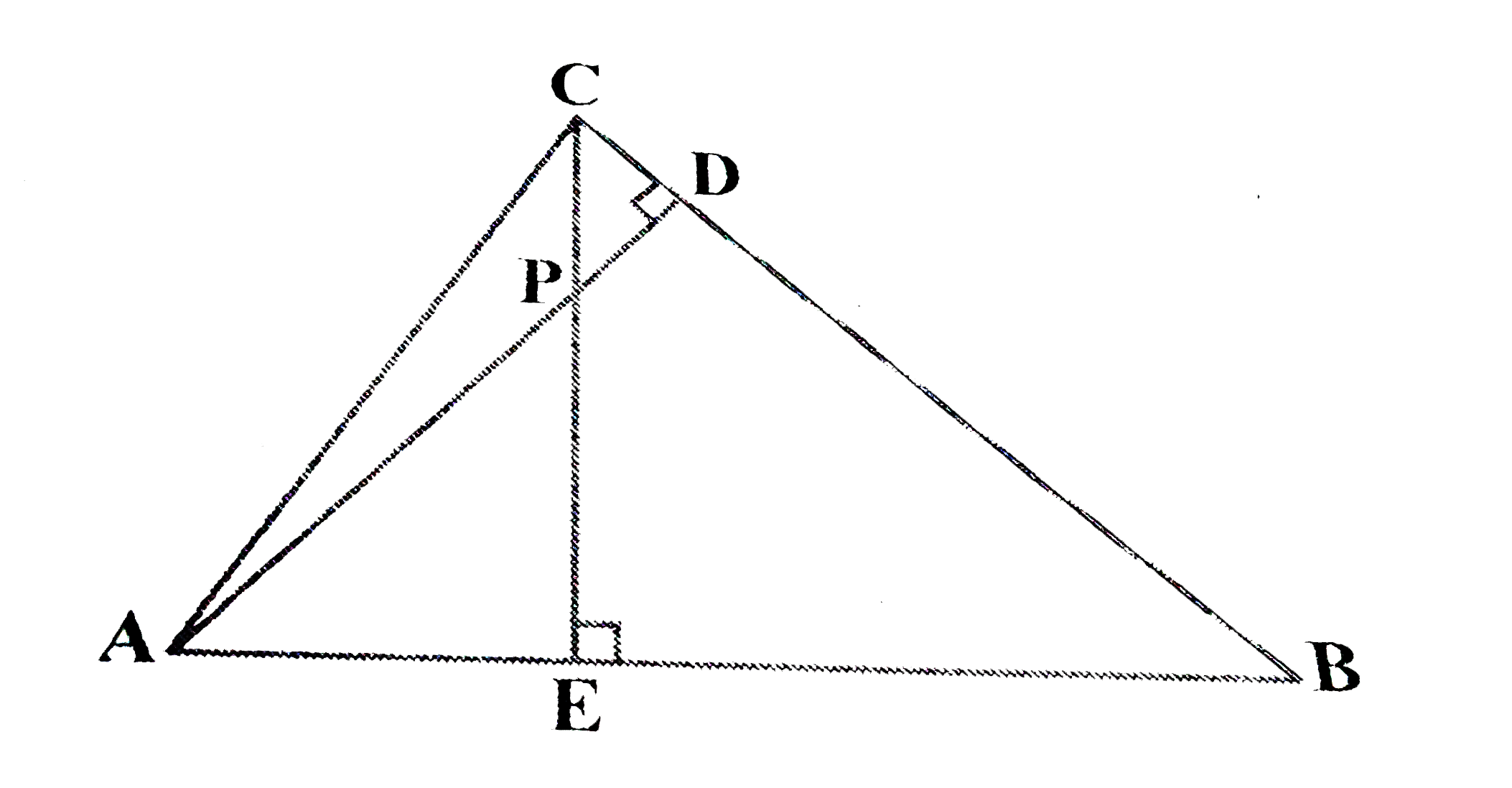
View SolutionIn Figure altitudes AD and CE of DABC intersect each other at the point P. Show that:
(i) ΔAEP~ΔCDP
(ii) ΔABD~ΔCBE
(iii) ΔAEP~ΔADB
(iv) ΔPDC~ΔBEC
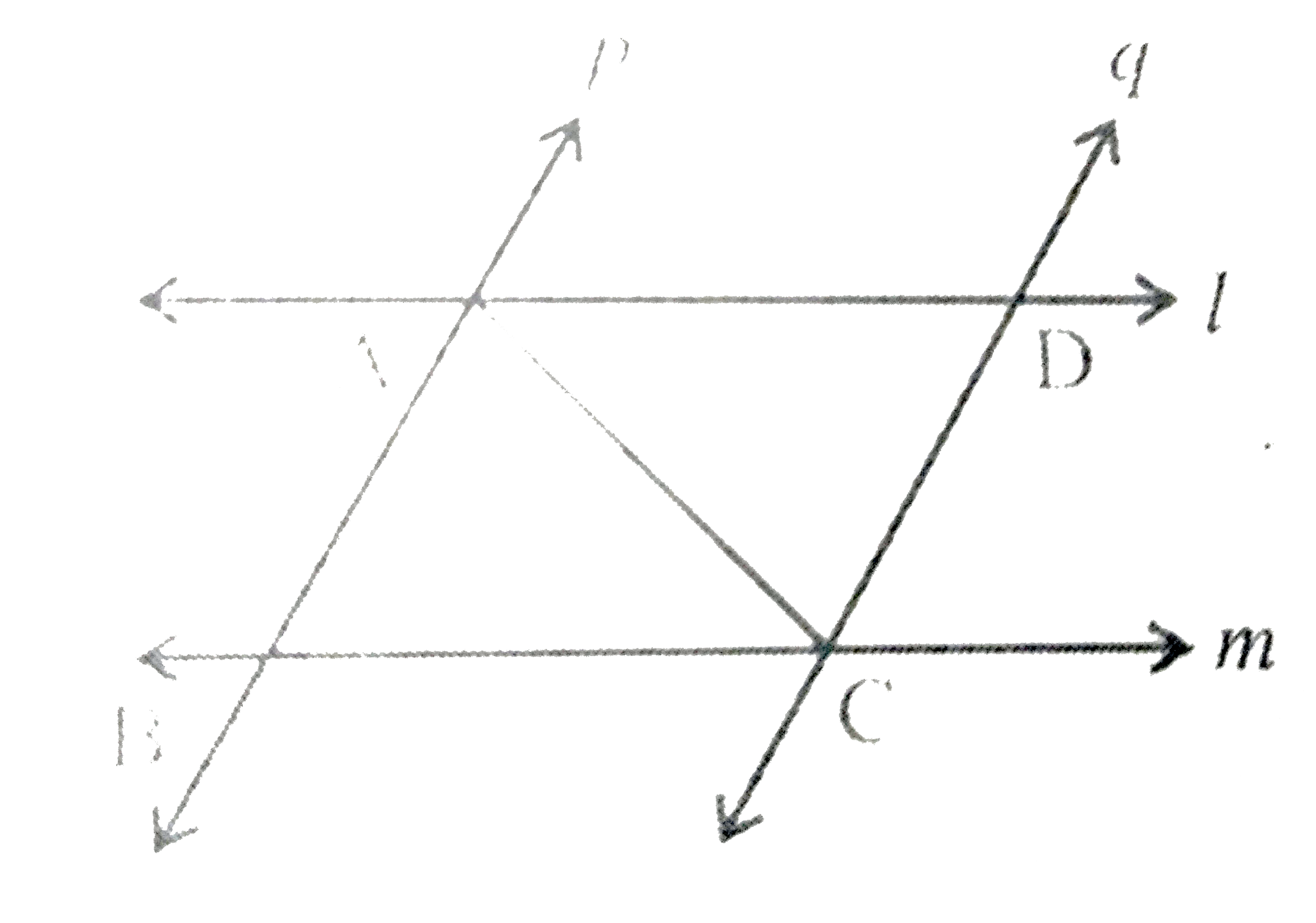
View Solutionl and m are two parallel lines intersected by another pair of parallel lines p and q (see Fig. 7.19). Show that ΔABC≅ΔCDA.
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that: CQ=13BC. Prove that AQCP is a parallelogram.
View SolutionABCD is a trapezium in which ABDC . P and Q are points on sides AD and BC such that PQAB . If PD=18 , BQ=35 and QC=15 , find AD .
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View Solution
