Derive formula for fringe width using Young's double slit method for interference of light. What will happen if the distance between the two slits becomes nearly zero ?
Fringe Width. It is the distance between any two successive fringes in interference pattern.
Let S1,S2 be the two fine slits illuminated by a monochromatic sources of wavelength λ.
Intensity of light at any point P on the screen at a distance D from the slit depends upon the path difference between S2P and S1P.
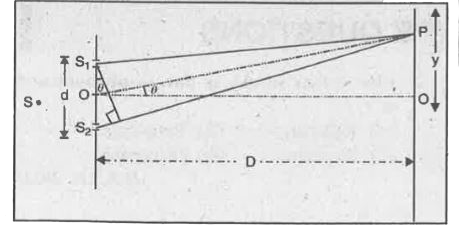
From S1 draw S1A perpendicular to S2P. Since ∠S2S1A→θ [D is very large as compared to d], therefore, ∠S1AS2→90∘ and AP≈S1P.
∴Path difference=S2P−S1P=(S2A+AP)−S1P or Path difference=S2A=dsinθ
Since θ is very small, sinθ can be replaced by tanθ .
∴Path difference=dtanθ=dyD
Constructive interference [Bright Fringes). For bright fringes, the path difference should be equal to an even multiple of λ/2.
∴dyD=2nλ2=nλ
or y=nλDd
If n = 0, y0=0, which is the position of central maxima.
If n = 1, y1=Ddλ, which is the position of first maxima.
If n = 2, y2=2Ddλ, which is the position of
Similarly yn−1=(n−1)Ddλ
and yn=nDdλ
Fringe width β=yn−y(n−1)=Ddλ[n−(n−1)]
β=Ddλ ...(i)
Destructive interference [Dark Fringes]. For dark fringes, the path difference should be an old multiple of 1/2.
dDy=(2n−1)λ2
or y=Dd(2n−1)λ2
If n = 1, y1=Ddλ2, which is the position of 1st minima.
If n = 2, y1=Dd2λ2, which is the position of 2nd minima.
If n = 3, y1=Dd3λ2, which is the position of 3rd minima.
∴ Fringe width, β=y3−y2=Ddλ
or β=Ddλ ...(ii)
From (i) and (ii), we conclude that bright and dark fringes have equal fringe width.
β∝D
∝λ
∝1d
If d = 0, β=∞ i.e. dark and bright bands will be infinitely well spaced and there will be uniform illumination.
Topper's Solved these Questions
Similar Questions
How does the fringe width, in Young's double-slit experiment, change when the distance of separation between the slits and screen is doubled ?
View SolutionIn Young's double slit experiment, the separation between the slits is halved and the distance between the slits and screen is doubled. The fringe-width will :
View Solution
Knowledge Check
In Young's double slit experiment, the interference bright fringes are of:
Aequal widths and unequal intensitiesBunequal width and equal intensitiesCequal widths and equal intensitiesDunequals widths and unequal intensitiesInterference fringes in Young's double slit experiment with monochromatic light are
Aalways equispacedBalways unequally spacedCboth equally and unequally spacedDformed by a portion of the wave front.In Young's double slit experiment, the separation between the slits is halved and the distance between the slits and screen is doubled. The fringe-width will :
AunchangedBhalvedCdoubledDquadrupled
In Young's double-slit experiment, the separation between the slits is halved and the distance between the slits and the screen in doubled. The fringe width is
View SolutionIn Young's double slit experiment, the sepcaration between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn young's double slit experiment, if the distance between the slits is halved and the distance between the slits and the screen is doubled, the fringe width becomes
View SolutionIn Young's double slit experiment, the distance between two slits is made three times then the fringe width will becomes
View SolutionIn Young's double slit interference experiment, the slit separation is made 3 fold. The fringe width becomes
View Solution

