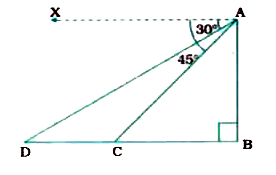
Two ships are sailing in the sea on the two sides of a lighthouse. The angles of elevation of the top of the lighthouse as observed from the two ships are 30o and 45o respectively. If the lighthouse is 100 m high, the distance between the two ships is (a) 173 m (b) 200 m (c) 273 m (d) 300 m
To solve the problem, we need to find the distance between two ships sailing on either side of a lighthouse, given the angles of elevation to the top of the lighthouse and its height.
Given:
- Height of the lighthouse (AB) = 100 m
- Angle of elevation from ship C (to the left) = 30°
- Angle of elevation from ship D (to the right) = 45°
1. Identify the triangles:
- From ship C, we have triangle ABC (where A is the top of the lighthouse, B is the base, and C is the position of the ship).
- From ship D, we have triangle ABD (where A is the top of the lighthouse, B is the base, and D is the position of the other ship).
2. Using Triangle ABC:
- In triangle ABC, we can use the tangent function:
tan(30°)=ABAC
- Here, AB=100 m (height of the lighthouse) and AC is the distance from the base of the lighthouse to ship C.
- We know that tan(30°)=1√3.
- Therefore:
1√3=100AC
- Rearranging gives:
AC=100√3 m
3. Using Triangle ABD:
- In triangle ABD, we apply the tangent function again:
tan(45°)=ABAD
- Here, AD is the distance from the base of the lighthouse to ship D.
- We know that tan(45°)=1.
- Therefore:
1=100AD
- Rearranging gives:
AD=100 m
4. Finding the total distance between the two ships (CD):
- The total distance between the two ships is the sum of AC and AD:
CD=AC+AD=100√3+100
- Factoring out 100:
CD=100(√3+1)
5. Calculating the numerical value:
- Using √3≈1.732:
CD≈100(1.732+1)=100(2.732)≈273.2 m
Conclusion:
The distance between the two ships is approximately 273 m. Thus, the correct option is (c) 273 m.
- Height of the lighthouse (AB) = 100 m
- Angle of elevation from ship C (to the left) = 30°
- Angle of elevation from ship D (to the right) = 45°
- From ship C, we have triangle ABC (where A is the top of the lighthouse, B is the base, and C is the position of the ship).
- From ship D, we have triangle ABD (where A is the top of the lighthouse, B is the base, and D is the position of the other ship).
- In triangle ABC, we can use the tangent function:
tan(30°)=ABAC
- Here, AB=100 m (height of the lighthouse) and AC is the distance from the base of the lighthouse to ship C.
- We know that tan(30°)=1√3.
- Therefore:
1√3=100AC
- Rearranging gives:
AC=100√3 m
- In triangle ABD, we apply the tangent function again:
tan(45°)=ABAD
- Here, AD is the distance from the base of the lighthouse to ship D.
- We know that tan(45°)=1.
- Therefore:
1=100AD
- Rearranging gives:
AD=100 m
- The total distance between the two ships is the sum of AC and AD:
CD=AC+AD=100√3+100
- Factoring out 100:
CD=100(√3+1)
- Using √3≈1.732:
CD≈100(1.732+1)=100(2.732)≈273.2 m
The distance between the two ships is approximately 273 m. Thus, the correct option is (c) 273 m.
Similar Questions
As observed from the top of a 75m high lighthouse from the sea-level, the angles of depression of two ships are 30∘and45∘. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships
View SolutionThe angle of depression of a ship as observed from the top of a lighthouse is 45∘ . If the height of the lighthouse is 200 m , then what is the distance of the ship from the foot of the lighthouse ?
View SolutionFrom the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 30∘. If the height of the lighthouse is 100 m, then find how far is that ship from the lighthouse.
View Solutionकिसी प्रकाशघर के विपरीत किनारों पर से देखने पर स्थित दो जहाजों के अवनमन कोण 30∘ तथा 45∘ देखे गए हैं यदि प्रकाशघर की ऊँचाई 300 मी हो और यदि उनको मिलाने वाली रेखा प्रकाशघर के आधार से गुजरती हो, तो जहाजों के बीच की दूरी है (√3=1.7321)
View Solutionकिसी प्रकाशधर के विपरीत किनारों पर से देखने पर स्थित दो जहाजों के अवनमन कोण 30∘ तथा 45∘ देखे गए हैं यदि प्रकाशघर की ऊँचाई 300 मी हो और यदि उनको मिलाने वाली रेखा प्रकाशघर के आधार से गुजरती हो, तो जहाजों के बीच की दूरी है ।
(√3=1.7321)
View Solutionएक लाइट हाउस से इसके विपरीत दिशाओं में स्थित दो जहाजों के अवनमन कोण क्रमशः 30∘ और 45∘ है यदि लाइट हाउस की ऊँचाई 100 m हो तो दोनों जहाजों के बीच की दूरी ज्ञात कीजिए यदि दोनों जहाजों को मिलाने वाली रेखा लाइट हाउस के पाद से जाती है।
View SolutionTwo ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is:
View SolutionTwo ships are sailling in the sea on the two sides of a lighthouse. If the distance between the ships is 10(√3+1) meters and their angle of elevations of the top of the lighthouse are 60∘and45∘, then the height of the lighthouse is (The two ships and the foot of lighthouse are in a straight line)
View Solution
