In an experiment on photoelectric effect, the slope of the cut-offf voltage versus frequency of incident light is found to be 4.12×10−15V s. calculate the value of Planck's constant.
As per Einstein.s photoelectric equation, slope of V0−v graph is he=4.12×10−15V s
∴Planck.s constant h=4.12×10−15×e=4.12×10−15×1.6×10−19=5.59×10−34Js.
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTERBOOK - U-LIKE SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - ADDITIONAL EXERCISES
15 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - U-LIKE SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - CASE BASED/SOURCE-BASED INTEGRATED QUESTIONS
10 Videos
- CURRENT ELECTRICITY BOOK - U-LIKE SERIESCHAPTER - CURRENT ELECTRICITY EXERCISE - SELF ASSESSMENT TEST (SECTION C )
3 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SELF ASSESSMENT TEST (SECTION-B) (VERY SHORT ANSWER QUESTIONS)
4 Videos
Similar Questions
(a) Estimate the speed with which electrons emitted from a heated emitter of an evacuated tube impinge on the collector maintained at a potential difference of 500 V with respect to the emitter. Ignore the small initial speeds of the electrons. The specific charge of the electron i.e., its e/m is given to be 1.76×1011C kg−1.
(b) Use the same formula you employ in (a) to obtain electron speed for an collector potential of 10 MV. do you see what is wrong ? In what way is the formula to be modified ?
View SolutionMetals have free electrons which are responsible for their conductivity. However, the free electron cannot normally escape out of the metal surface. If an electron attempts to come out of the metal, the metal surface acquires a positive charge and pulls the electron back to the metal. an electron can come out of the metal surface only if it has got sufficient energy to overcome the attractive pull of ions present in metal. thus, a certain minimum amount of energy is required to be given to an electron to pull it out from the surface of the metal. this minimum energy required by an electron to escape from the metal surface is called the work function of the metal.
Following table gives the work function (ϕ0) of some metals:

On the basis of data given in the above table and your understanding of the related concepts answer the following questions:
Q. How is energy equal to work function supplied to a metal in photoelectric emission?
View SolutionState Kirchhoff's rules of current distribution in an electrical network. Using these rules determine the value of the current I1 in the electric circuit of Fig.
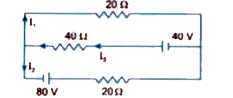
View SolutionThree small , identical point charges lie on the circumference of a circle forming an equilateral triangle.Calculate the value of electric field at the centre of circle.
View SolutionIn an experiment on photoelectric effect, the slope of the cut off voltage versus frequency of incident light is found to be 4.12×10−15Vs. Given e=1.6×10−19C, estimate the value of Planck's constant.
View SolutionIn a photoelectric experiment, the graph of frequency v of incident light (in Hz) and stopping potential V (in V) is as shown in the figure. Planck's constant is (e is the elementary charge)
View Solutionप्रकाश विद्युत प्रभाव के एक प्रयोग में प्रकाश आवृत्ति के विरूद्ध अंतक वोल्टता की ढलान 4.12×10−15Vs प्राप्त होती है। प्लांक स्थिरांक का मान परिकलित कीजिए।
View Solutionप्रकाशवैधुत प्रभाव के एक प्रयोग में, प्रकाश आवृत्ति के विरुध्द अंतक वोल्टता कि ढलान 4.12×10−15Vs प्राप्त होती है । प्लांक स्थिरांक का मान परिकलित कीजिए ।
View SolutionIn photoelectric effect the slope of straight line graph between stopping potential (V_(s)) and frequency of incident light (v) gives
View SolutionFor photoelectronic effect in sodium, the figure shows the plot of cut-off voltage versus frequency of incident radiation. Calculate threshold frequency
View SolutionFor photoelectric effect in sodium, the figure shows the plot of cut-off voltage versus frequency of incident radiation. Calculate threshold frequency
View SolutionIn an experiment on the photoelectric effect , the slope of the cut - off voltage versus frequency of incident light is found to be 4.12xx10^(-15) V s . The value of Planck's constant is
View SolutionIn an experiment on photo electric effect, the slope of cut - off voltage versus frequency, incident light is found to be 4.12×10−15 Vs. Calculate the of Planck's constant.
View SolutionIn photoelectric effect the slope of stop of stopping potential versus frequency of incident light for a given surface will be
View SolutionIn photoelectric effect the slope of stop of stopping potential versus frequency of incident light for a given surface will be
View SolutionIn an experiment on photoelectric effect, the slope of the cut off voltage versus frequency of incident light is found to be 4.12xx10^(-15)Vs . Given e=1.6xx10^(-19)C , estimate the value of Planck's constant.
View Solution

