Let S=S1∩S2∩S3, where s1={z∈C|z∣<4},S2={z∈C:ln[z−1+√3i1−√31]>0}andS3={z∈C:Rez>0}
0
1
2
∞
The correct Answer is:B
Let z=x+iy
Set A corresponds to the region y≤1
Set B consists of points lying on the circle center at (2,1) and readius 3
i.e x2+y2y−4
Set C consistes of points lying on the x+y=√2
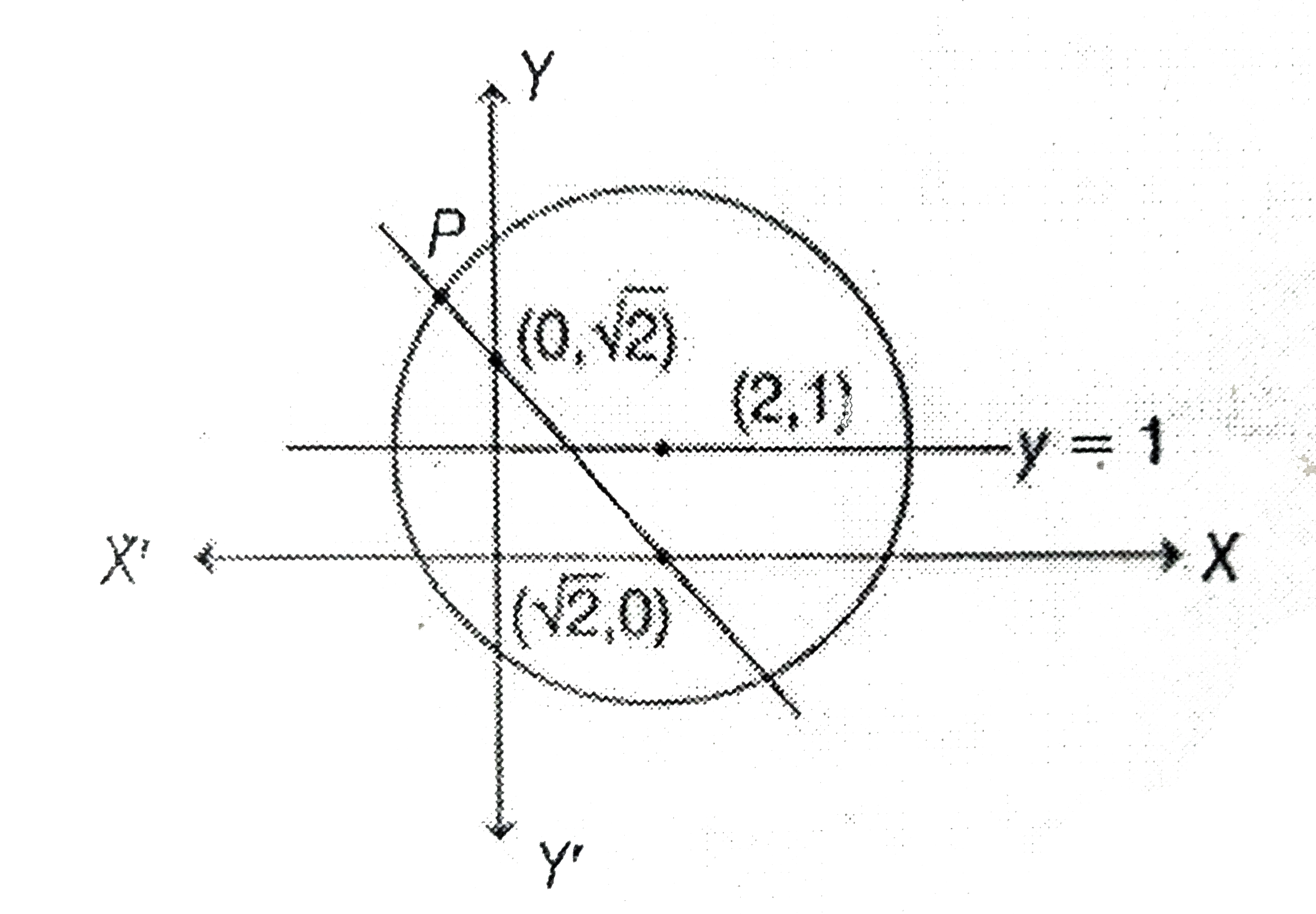 Clearly there is only one point of the line x+y=√2 and circlex2+y2−4x2y=4
Clearly there is only one point of the line x+y=√2 and circlex2+y2−4x2y=4
Topper's Solved these Questions
- COMPLEX NUMBERSBook:IIT JEE PREVIOUS YEARChapter:COMPLEX NUMBERSExercise:TOPIC 2 CONJUGATE AND MODULUS OF A COMPLEX NUMBER (MATCH THE COLUMNS)
Explore 1 Video
- COMPLEX NUMBERSBook:IIT JEE PREVIOUS YEARChapter:COMPLEX NUMBERSExercise:TOPIC 2 CONJUGATE AND MODULUS OF A COMPLEX NUMBER (FILL IN THE BLANKS )
Explore 3 Videos
- COMPLEX NUMBERSBook:IIT JEE PREVIOUS YEARChapter:COMPLEX NUMBERSExercise:TOPIC 2 CONJUGATE AND MODULUS OF A COMPLEX NUMBER (PASSAGE BASED PROBLEMS )(PASSAGE I)
Explore 3 Videos
- CIRCLEBook:IIT JEE PREVIOUS YEARChapter:CIRCLEExercise:Topic 5 Integer Answer type Question
Explore 1 Video
- DEFINITE INTEGRATIONBook:IIT JEE PREVIOUS YEARChapter:DEFINITE INTEGRATIONExercise:LIMITS AS THE SUM
Explore 6 Videos
Similar Questions
Match the statements of Column I with those of Column II
Here ,z takes values in the complex plane and Im (z) and Re(z) denote respectively , the imaginary part and the real part of z
View SolutionIf α,β,γ are the cube roots of p, then for any x,y,z xα+yβ+zγxβ+yγ+zα =
View SolutionLet A,B,C be three sets of complex number as defined below
A={z:lm(z)≥1}
B={z|z−2−i∣=3}
C={z:Re((1−i)z)=√2}
minz∈s|1−3i−z| is equal to
View SolutionTwo parallel chords of a circle of radius 2 are at a distance √3+1 apart. If the chord subtend angles πkand2πk at the center, where k>0, then the value of [k] is _____
View Solutionlimn→∞((n+1)1/3n4/2+(n+2)1/3n4/3+....+(2n)1/3n4/3) is equal to
View SolutionLet S=S_(1)nn S_(2)nn S_(3), where s_(1)={z in C:|z| 0} and S_(3)={z in C:Re z>0
View SolutionIf z=(√32+12i)5+(√32−i2)5, then (a) im(z)=0 (b) Re(z)>0,Im(z)>0 (c) Re(z)>0,Im(z)<0 (d) Re(z)=3
View SolutionLet S=S1∩S2∩S3 where
S1={z∈C|z∣<4},S2={z∈C:lm[z−1+√3i1−√3i]>0} and S3:{z∈:Rez<0}
Let z be any point in A∩B∩C
The |z+1−i|2+|z−5−i|2 lies between
View Solutionमाना A, B, C सम्मिश्र संख्याओं के तीन समुच्चय है जो निम्न प्रकार से परिभाषित है।
A={z:Imz≥1}
B={z:|z−2−i|=3}
C={z:Re(1−i)z)=√2}
समुच्चय A∩B∩C में अवयवों की संख्या है
View Solutionमाना कि S=S1∩S2∩S3, जहाँ S1={z∈C:|z|<4},S2={z∈C:Im[z−1+√3i1−√3i>0} तथा S3={z∈C:Rez>0}
z∈S––––––(Min)|1−3i−z|=
View SolutionLet the sum of n, 2n, 3n terms of an A.P. be S1,S2andS3 , respectively, show that S3=3(S2−S1)
View SolutionLet the sum of n, 2n, 3n terms of an A.P. be S1,S2andS3 , respectively, show that S3=3(S2−S1)
View SolutionLet the sum of n, 2n, 3n terms of an A.P. be S1,S2andS3 , respectively, show that S3=3(S2−S1)
View SolutionLet the sum of n, 2n, 3n terms of an A.P. be S1,S2and S3, respectively, show that S3=3(S2−S1).
View Solutionमाना कि S=S1∩S2∩S3 जहां S1=[z∈C|z∣<4},S2={z∈C:Im[z−1+√3i1−√3i]>0} तथा S3={z∈C:Rez>0}
S का क्षेत्रफल =
View Solutionमाना कि S=S1∩S2∩S3 जहां S1=[z∈C|z∣<4},S2={z∈C:Im[z−1+√3i1−√3i]>0} तथा S3={z∈C:Rez>0}
minZ∈S|1−3i−z|=
View Solution
