A plane EM wave travelling along z - direction is desctribed →E=E0sin(kz−ωt)ˆi and veC(B)=B0sin(kz−ω)ˆj. Show that
The time averaged intensity of the wave is given by Iav=12c∈0E20. Solution in Gujrati
Radiant flux density,
S=1μ0(→E×→B)
∴S=c2∈0(→E×→B) …(1)[∵c=1√μ0∈0]
Let electromagnetic waves propagate in x - direction. Electric field vector in y - direction and magnetic field vector in z - direction. Hence,
→E=→E0cos(kx−ωt)
→B=→B0cos(kx−ωt)
→E×→B=(→E0×→B0)cos2(kx−ωt)
S=c2∈0(→E×→B) [∵ From equation (1)]
c2∈0(→E0×→B0)cos2(kx−ωt)
Average value of magnitude of radiant flux density over complete cycle is,
Saverage=c2∈0∣∣→E0×→B0∣∣1T∫T0cos2(kx−ωt)dt
c2∈0E0B0×1T×T2 [∵∣∣→E0×→B0∣∣=E0B0sin90∘=E0B0]
and ∫T0cos2(kx−ωt)dt=T2
∴Saverage=c22.∈0E0(E0c) [∵c=E0B0⇒B0=E20c]
=c2∈0E20
=c2×1c2μ0×E20 [∵c=1√μ0∈0⇒∈0=1c2μ0]
=E202μ0c
Similar Questions
A plane EM wave travelling in vacuum along z - direction is given by vec(E )=E_(0)sin (kz - omega t)hat(i) and vec(B)=B_(0)sin(kz - omega t)hat(j) . Evaluate int vec(B).vec(d)s over the surface bounded by loop 1234.
View SolutionA plane EM wave travelling in vacuum along z - direction is given by →E=E0sin(kz−ωt)ˆi and →B=B0sin(kz−ωt)ˆj.
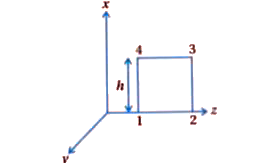
Use equation ∫→E.→dl=−dϕBdt to prove E0B0=c.
View SolutionA plane EM wave travelling in vacuum along z - direction is given by vec(E )=E_(0)sin (kz - omega t)hat(i) and vec(B)=B_(0)sin(kz - omega t)hat(j) . By using similar process and the equation int vec(B).vec(d)l = mu_(0)I+ in_(0)(d phi_(E ))/(dt) , prove that c=(1)/(sqrt(mu_(0)in_(0)))
View SolutionA plane EM wave travelling along z - direction is desctribed vec(E )=E_(0)sin(kz - omega t)hat(i) and veC(B)=B_(0)sin (kz - omega)hat(j) . Show that The average energy density of the wave is given by U_(av)=(1)/(4)in_(0)E_(0)^(2)+(1)/(4).(B_(0)^(2))/(mu_(0)) .
View SolutionA plane EM wave travelling along z - direction is desctribed →E=E0sin(kz−ωt)ˆi and veC(B)=B0sin(kz−ω)ˆj. Show that
The time averaged intensity of the wave is given by Iav=12c∈0E20.
View Solutionदो तरंगे E1=E0sinωt और E2sin(ωt+60∘) व्यतिकरण करती है तो परिणामी तरंग की प्रारम्भिक कला होगी :-
View SolutionZदिशा के अनुदिश गतिमान एक समतल वैधुतचुमबकीय तरंग को E=E0sin(kz–εt)ˆIतथाB=B0sin(kz–εt)ˆj द्वारा वर्णित किया गया है। दर्शाइए कि
(i) तरंग का औसत ऊर्जा घनत्व है।
μav=14E0E20+14.B20μ0
(ii) तरंग की काल – ओसत तीव्रता है।
Iav=12CE0E20
View SolutionMagnetic waves oscillating along the z-axis E=E_(0) cos (kz - omega t) Displayed by, choose the correct statement.
View Solution

