If R denotes circumradius, then in ΔABC,b2−c22aR is equal to
The correct Answer is:(sin(B−C))
To solve the problem, we need to find the value of b2−c22aR in triangle ABC, where R is the circumradius.
1. Understanding the Circumradius:
The circumradius R of triangle ABC can be expressed in terms of the sides and angles of the triangle. We know that:
R=a2sinA
2. Using the Sine Rule:
According to the sine rule, we have:
asinA=bsinB=csinC=k
From this, we can express the sides in terms of k:
a=ksinA,b=ksinB,c=ksinC
3. Substituting for R:
We substitute R into our expression:
b2−c22aR=b2−c22a⋅a2sinA=b2−c2a2sinA=(b2−c2)sinAa2
4. Expressing b2−c2:
We can use the identity b2−c2=(b−c)(b+c). Thus, we need to express b and c in terms of k:
b=ksinB,c=ksinC
Therefore:
b2−c2=k2(sin2B−sin2C)
5. Using the Sine Difference Identity:
We can apply the sine difference identity:
sin2B−sin2C=(sinB−sinC)(sinB+sinC)
6. Substituting Back:
Now substituting back into our expression:
(b2−c2)sinAa2=k2(sinB−sinC)(sinB+sinC)sinAa2
7. Final Expression:
Since a=ksinA, we can express a2 as:
a2=k2sin2A
Thus, we have:
(b2−c2)sinAa2=(sinB−sinC)(sinB+sinC)sinAsin2A
8. Result:
Finally, using the sine difference and sum identities, we find:
b2−c22aR=sin(B−C)
Conclusion:
Thus, we conclude that:
b2−c22aR=sin(B−C)
The circumradius R of triangle ABC can be expressed in terms of the sides and angles of the triangle. We know that:
R=a2sinA
According to the sine rule, we have:
asinA=bsinB=csinC=k
From this, we can express the sides in terms of k:
a=ksinA,b=ksinB,c=ksinC
We substitute R into our expression:
b2−c22aR=b2−c22a⋅a2sinA=b2−c2a2sinA=(b2−c2)sinAa2
We can use the identity b2−c2=(b−c)(b+c). Thus, we need to express b and c in terms of k:
b=ksinB,c=ksinC
Therefore:
b2−c2=k2(sin2B−sin2C)
We can apply the sine difference identity:
sin2B−sin2C=(sinB−sinC)(sinB+sinC)
Now substituting back into our expression:
(b2−c2)sinAa2=k2(sinB−sinC)(sinB+sinC)sinAa2
Since a=ksinA, we can express a2 as:
a2=k2sin2A
Thus, we have:
(b2−c2)sinAa2=(sinB−sinC)(sinB+sinC)sinAsin2A
Finally, using the sine difference and sum identities, we find:
b2−c22aR=sin(B−C)
Thus, we conclude that:
b2−c22aR=sin(B−C)
Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - PROPERTIES AND SOLUTIONS OF TRIANGLES EXERCISE 7 : SUBJECTIVE TYPE QUESTIONS
10 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - PROPERTIES AND SOLUTIONS OF TRIANGLES EXERCISE 6 : SINGLE INTEGER ANSWER TYPE QUESTIONS
1 Video
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
A hexagon is inscribed in a circle of radius r. Two of its sides have length 1, two have length 2 and the last two have length 3. Prove that r is a root of the equation 2r3−7r−3=0.
View SolutionIn a triangle XYZ, let x, y, z be the lengths of sides opposite to the angles X, Y, Z, respectively, and 2s = x + y + z. If s−x4=s−y3=s−z2 of incircle of the triangle XYZ is 8π3
View SolutionIn the figure as shown find the number of digits in the length of AB.
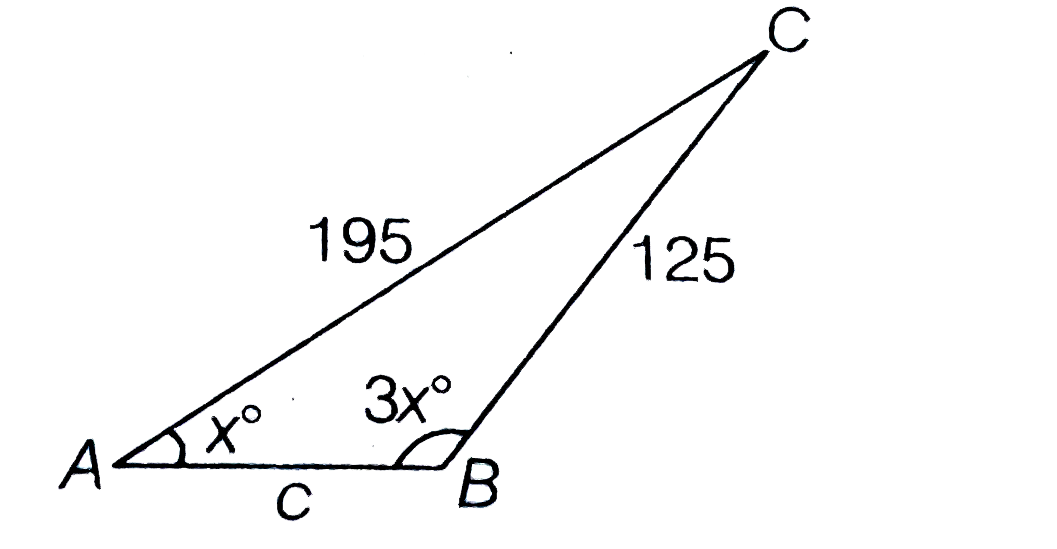
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View SolutionIf R denotes circumradius,then in Delta ABC,(b^(2)-c^(2))/(2aR) is equal to
View SolutionIf the area of the triangle ABC is a^(2)-(b-c)^(2), then its circumradius R=
View SolutionIf the area of the triangle ABC is a^(2)-(b-c)^(2) then its circumradius R is
View SolutionIn triangle ABC, let ∠C=π/2. If r is the inradius and R is circumradius of the triangle, then 2(r+R) is equal to
View SolutionIn ΔABC,∠C=2∠A,andAC=2BC, then the value of a2+b2c2R2 (where R is circumradius of triangle) is ______
View SolutionIf Δ denotes the area of ΔABC, then b2sin2C+c2sin2B is equal to
View SolutionIf R denotes the circum-radius of a ΔABC, then b2−c22aR is equal to
View SolutionIF the area of the triangle ABC is a2−(b−c)2, then its circumradius R=
View SolutionLet R be the circumradius of ΔABC. Then b2−c22aR equals
View SolutionIn triangle ABC, let ∠C=π/2. If r is the inradius and R is circumradius of the triangle, then 2(r+R) is equal to
View Solution

