If Δ=a2−(b−c)2,Δ is the area of the ΔABC then tanA= ?
The correct Answer is:(815)
To solve the problem, we need to find the value of tanA given that the area Δ of triangle ABC is expressed as:
Δ=a2−(b−c)2
1. Express the Area in Terms of Sides:
We know that the area Δ of triangle ABC can also be expressed using the formula:
Δ=12absinC
However, we will first manipulate the expression given in the problem.
2. Rewrite the Expression:
The expression for Δ can be simplified:
Δ=a2−(b−c)2
This can be factored using the difference of squares:
Δ=(a+(b−c))(a−(b−c))=(a+b−c)(a−b+c)
3. Relate to Semi-Perimeter:
In triangle geometry, we know that:
s=a+b+c2
Therefore, we can express a+b−c and a−b+c in terms of s:
a+b−c=(s+c)anda−b+c=(s+b)
So we can rewrite Δ:
Δ=(s+c)(s+b)
4. Using the Area Formula:
We know that the area can also be expressed in terms of the semi-perimeter s:
Δ=√s(s−a)(s−b)(s−c)
Equating the two expressions for Δ:
(s+c)(s+b)=√s(s−a)(s−b)(s−c)
5. Finding tanA:
We can use the relation:
tanA2=(s−b)(s−c)s(s−a)
Given that Δ=14, we can substitute this into the formula for tanA2:
tanA2=14
6. Using the Double Angle Formula:
We know that:
tanA=2tanA21−tan2A2
Substituting tanA2=14:
tanA=2⋅141−(14)2=121−116=121516=12⋅1615=815
Final Answer:
Thus, the value of tanA is:
815
We know that the area Δ of triangle ABC can also be expressed using the formula:
Δ=12absinC
However, we will first manipulate the expression given in the problem.
The expression for Δ can be simplified:
Δ=a2−(b−c)2
This can be factored using the difference of squares:
Δ=(a+(b−c))(a−(b−c))=(a+b−c)(a−b+c)
In triangle geometry, we know that:
s=a+b+c2
Therefore, we can express a+b−c and a−b+c in terms of s:
a+b−c=(s+c)anda−b+c=(s+b)
So we can rewrite Δ:
Δ=(s+c)(s+b)
We know that the area can also be expressed in terms of the semi-perimeter s:
Δ=√s(s−a)(s−b)(s−c)
Equating the two expressions for Δ:
(s+c)(s+b)=√s(s−a)(s−b)(s−c)
We can use the relation:
tanA2=(s−b)(s−c)s(s−a)
Given that Δ=14, we can substitute this into the formula for tanA2:
tanA2=14
We know that:
tanA=2tanA21−tan2A2
Substituting tanA2=14:
tanA=2⋅141−(14)2=121−116=121516=12⋅1615=815
Thus, the value of tanA is:
815
Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - PROPERTIES AND SOLUTIONS OF TRIANGLES EXERCISE 7 : SUBJECTIVE TYPE QUESTIONS
10 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - PROPERTIES AND SOLUTIONS OF TRIANGLES EXERCISE 6 : SINGLE INTEGER ANSWER TYPE QUESTIONS
1 Video
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
A hexagon is inscribed in a circle of radius r. Two of its sides have length 1, two have length 2 and the last two have length 3. Prove that r is a root of the equation 2r3−7r−3=0.
View SolutionIn a triangle XYZ, let x, y, z be the lengths of sides opposite to the angles X, Y, Z, respectively, and 2s = x + y + z. If s−x4=s−y3=s−z2 of incircle of the triangle XYZ is 8π3
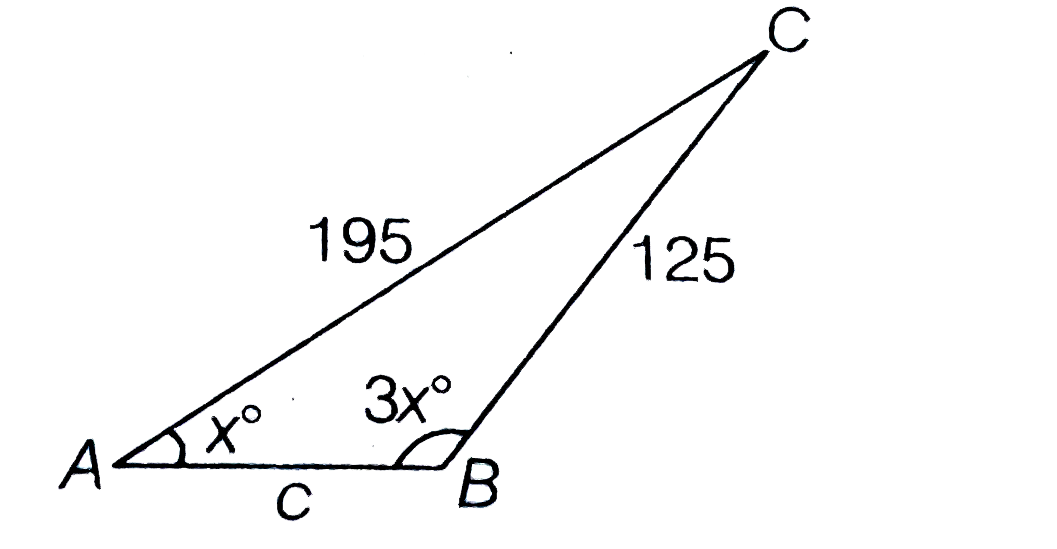
View SolutionIn the figure as shown find the number of digits in the length of AB.
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View SolutionThe area Delta of a triangle ABC is given by Delta=a^(2)-(b-c)^(2) then tan((A)/(2))=
View SolutionIn Delta ABC, area of incircle : area of Delta ABC=pi:T san((A)/(2))tan((B)/(2))tan((C)/(2))
View SolutionIn a ΔABC,tanA+tanB+tanC=6andtanAtanB=2, then the triangle ABC is
View SolutionIf Δ=a2−(b−c)2,Δ is the area of the ΔABC then tanA= ?
View SolutionIf Δ=a2−(b−c)2, whereΔ is the area of the triangle ABC, then tan A is equal to-
View SolutionIf the area of a triangle ABC is given by Δ=a2−(b−c)2, then tan.A2 is equal to
View SolutionIf the area Δ of ΔABC is given by Δ=a2−(b−c)2, then : tan A =
View SolutionIf Δ=a2−(b−c)2, is the area of the triangle ABC, then tan A=
View SolutionIf the area of triangle ABC is b2−(c−a)2 then tan B=
View SolutionIf Δ=a2−(b−c)2 where Δ is the area of triangle ABC then tan A is equal to
View Solution

