The state of an ideal gas is changed through an isothermal process at temperature T0 as shown in the figure. The work done by the gas in going from state B to C is double the work done by the gas in going from state A to B. IF the pressure in the state B is p0/2, then the pressure of the gas in state C is

P02
P04
P06
P08
Work done by gas in going isothermally from state A to B is
ΔWAB=nRTlnPAPC=nRTln2 .....(1)
Work done by gas in going isothermally from state B to C is
ΔWBC=nRTlnPBPC=nRTlnP02PC.....(2)
It is given that ΔWBC=2ΔWAB
∴lnP02PC=ln(2)2∴Pc=P08
Topper's Solved these Questions
Similar Questions
The state of an ideal gas is changed through an isothermal process at temperature T0 as shown in figure. The work done by the gas in going from state B to C is double the work done by gas in going from state A to B. If the pressure in the state B is p02, then the pressure of the gas in state C is
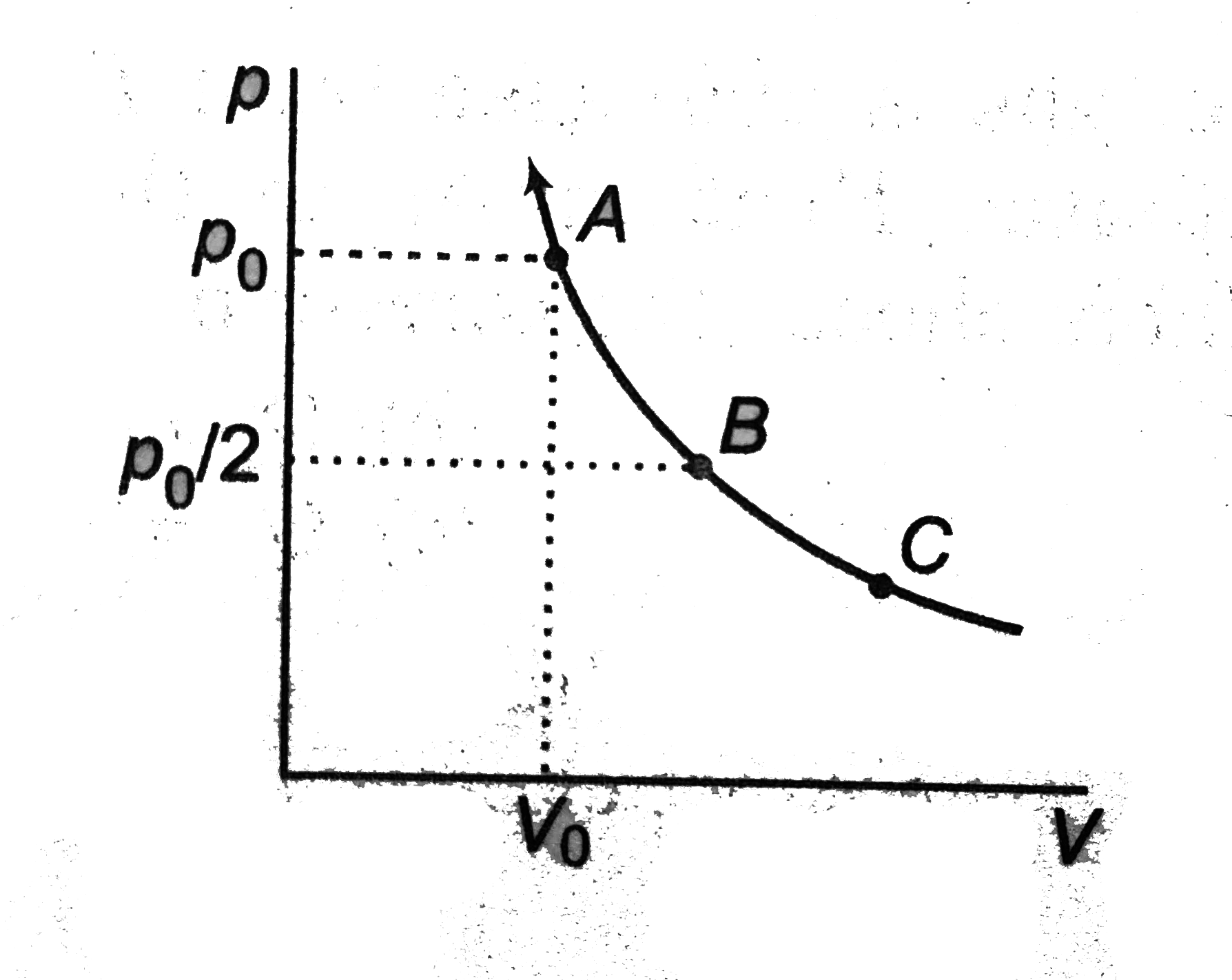
View SolutionThe state of an ideal gas is changed through an isothermal process at temperature T0 as shown in figure. The work done by the gas in going from state B to C is double the work done by gas in going from state A to B. If the pressure in the state B is p02, then the pressure of the gas in state C is

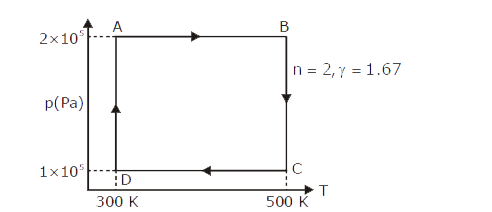
View SolutionAssume the gas to be ideal, the work done on the gas in taking it from A to B is
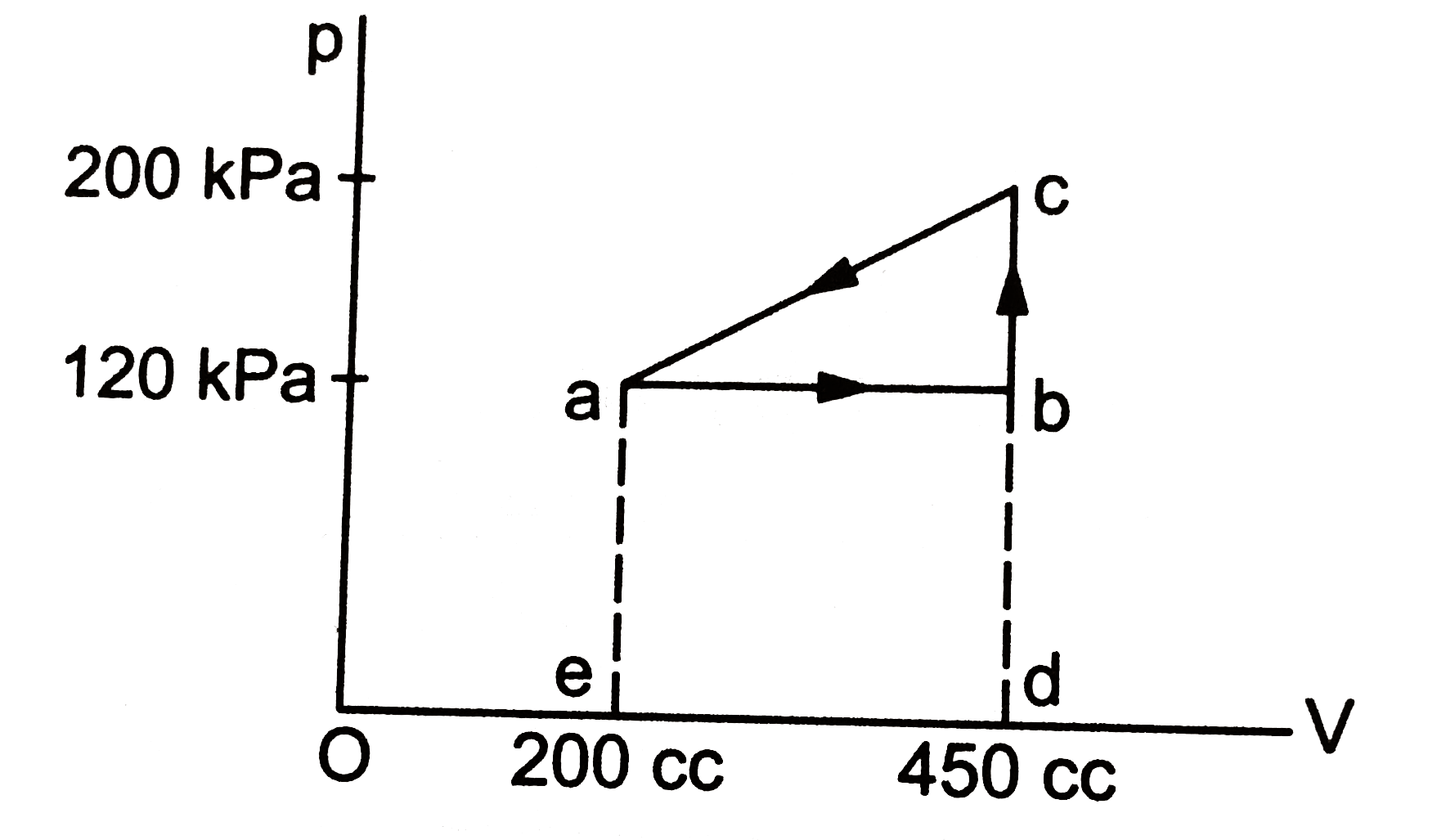
View SolutionCalculate the work done by the gas in the state diagram shown :

View SolutionIf a system undergoes an adiabatic change from state 1 to state 2, the work done by the gas is:
View Solutioncalculate the work done by a gas as it is taken from the state a to b, b to c and c to a as shown in
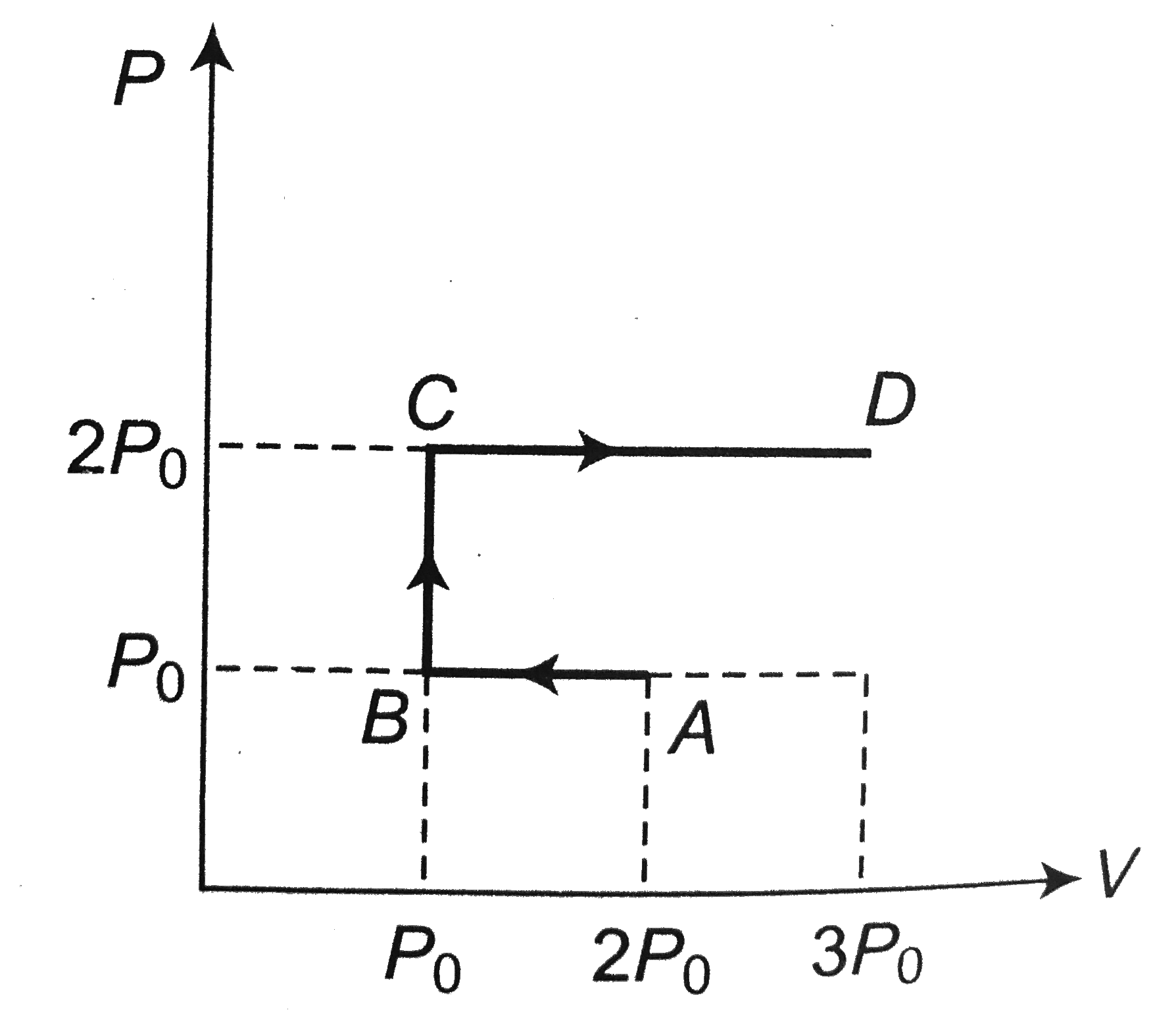
View SolutionP−V diagram of an ideal gas is as shown in figure. Work done by the gas in process ABCD is
View SolutionAn ideal gas change from state a to state b as shown in Fig. what is the work done by the gas in the process?

View Solution1.0 mol of a monoatomic ideal gas is expanded from state (1) to state (2) as shown in figure. Calculate the work done for the expansion of gas from state (1) to state (2) at 298 K.

View SolutionThe volume (V) of a monatomic gas varies with its temperature (T) as shown in the graph. The ratio of work done by the gas, to the heat absorbed by it, when it undergoes a change from state A to state B,is
View Solution
