A fresh dry cell of 1.5 volt and two resistors of 10kΩ each are connected in series. An analog voltmeter measures a voltage of 0.5 volt across each of the resistor. A 100μF capacitor is fully charged using the same source. The same voltmeter is now used to measure the voltage across It. The initial value of the current and the time in which the voltmeter reading falls to 0.5 volt are respectively.
60μA,11s
120μA,15s
150μA,m15s
150μA,11s
The correct Answer is:D
To solve the problem step by step, we will analyze the circuit and use the relevant formulas.
Step 1: Understand the Circuit Configuration
We have a fresh dry cell of 1.5 volts connected in series with two resistors, each of 10 kΩ. The total resistance in the circuit is:
Rtotal=R1+R2=10kΩ+10kΩ=20kΩ
Step 2: Calculate the Total Current in the Circuit
Using Ohm's law, the total current I in the circuit can be calculated as:
I=VRtotal=1.5V20kΩ
Converting 20kΩ to ohms:
20kΩ=20,000Ω
Now substituting the values:
I=1.520000=0.000075A=75μA
Step 3: Analyze the Voltmeter Reading
The voltmeter measures 0.5 volts across each resistor. This indicates that the voltmeter is also part of the circuit and has some internal resistance. The reading across each resistor confirms that the circuit is functioning correctly.
Step 4: Charging the Capacitor
A capacitor of 100μF is charged using the same source. When the capacitor is fully charged, it will have the same voltage as the source, which is 1.5 volts.
Step 5: Determine the Initial Current through the Capacitor
When the capacitor is first connected, it behaves like a short circuit, and the initial current I0 can be calculated using:
I0=VR
Where R is the total resistance in the circuit, which is still 20kΩ:
I0=1.5V20kΩ=75μA
Step 6: Calculate the Time for the Voltage to Fall to 0.5 Volts
The voltage across a charging capacitor can be described by the equation:
V(t)=V0(1−e−tRC)
Where:
- V0=1.5V (initial voltage)
- V(t)=0.5V (voltage after time t)
- R=20kΩ=20000Ω
- C=100μF=100×10−6F
First, calculate RC:
RC=20000Ω×100×10−6F=2seconds
Now, substituting into the voltage equation:
0.5=1.5(1−e−t2)
Rearranging gives:
0.51.5=1−e−t2
13=1−e−t2
e−t2=1−13=23
Taking the natural logarithm:
−t2=ln(23)
t=−2ln(23)
Calculating t:
t≈−2×(−0.4055)≈0.811seconds
Final Results
The initial current is 75μA and the time for the voltmeter reading to fall to 0.5 volts is approximately 0.811seconds.
We have a fresh dry cell of 1.5 volts connected in series with two resistors, each of 10 kΩ. The total resistance in the circuit is:
Rtotal=R1+R2=10kΩ+10kΩ=20kΩ
Using Ohm's law, the total current I in the circuit can be calculated as:
I=VRtotal=1.5V20kΩ
Converting 20kΩ to ohms:
20kΩ=20,000Ω
Now substituting the values:
I=1.520000=0.000075A=75μA
The voltmeter measures 0.5 volts across each resistor. This indicates that the voltmeter is also part of the circuit and has some internal resistance. The reading across each resistor confirms that the circuit is functioning correctly.
A capacitor of 100μF is charged using the same source. When the capacitor is fully charged, it will have the same voltage as the source, which is 1.5 volts.
When the capacitor is first connected, it behaves like a short circuit, and the initial current I0 can be calculated using:
I0=VR
Where R is the total resistance in the circuit, which is still 20kΩ:
I0=1.5V20kΩ=75μA
The voltage across a charging capacitor can be described by the equation:
V(t)=V0(1−e−tRC)
Where:
- V0=1.5V (initial voltage)
- V(t)=0.5V (voltage after time t)
- R=20kΩ=20000Ω
- C=100μF=100×10−6F
RC=20000Ω×100×10−6F=2seconds
0.5=1.5(1−e−t2)
Rearranging gives:
0.51.5=1−e−t2
13=1−e−t2
e−t2=1−13=23
−t2=ln(23)
t=−2ln(23)
t≈−2×(−0.4055)≈0.811seconds
The initial current is 75μA and the time for the voltmeter reading to fall to 0.5 volts is approximately 0.811seconds.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.57
8 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.58
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.55
8 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A shell of mass 4kg moving with a velocoity 10m/s vertically upward explodes into three parts at a height 50m from ground. After three seconds, one part of mass 2kg reaches ground and another part of mass 1kg is at height 40m from ground. The height of the third part from the ground is : [g=10m/s2]
View SolutionIn the circuit shown in fig. XC=100Ω,(XL)=200ΩandR=100Ω. The effective current through the source is

View SolutionThe circuit was in the shown state for a long time. Now if the switch S is closed then the net charge that flows through the switch S, will be

View SolutionA galvanometer having 30 divisions has a current sensitivity of 20μA/ division. It has a resistance of 5Ω How will you convert it into an ammeter measuring upto 1A ?
View SolutionAn electromagnetic wave of frequency υ=3 MHz passes from vacuum into a dielectric medium with permittivity ε=4. Then
View SolutionA voltmeter of resistances 400(Ω)is used to measure the potential difference across the 100(Ω)resistor in the circuit shown in figure.(a) What will be the reading of the voltmeter ?(b) What was the potential difference across 100(Ω)before the voltmeter was connected ?
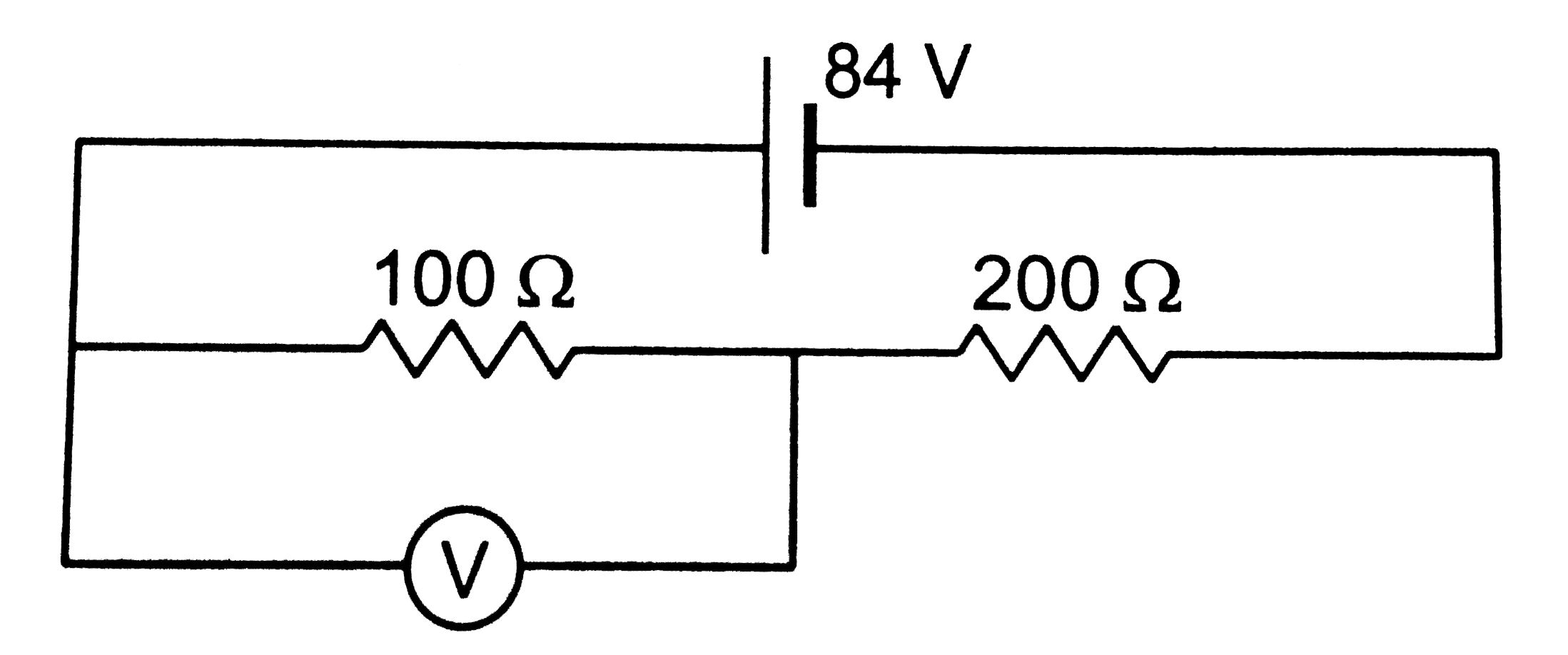
View Solution50Ω and 100Ω resistors are connected in series. This connection is connected with a battery of 2.4 volts. Whne a voltmeter, then the reading of the voltmeter will be 100Ω resistor, then eh reading of the voltmeter will be
View SolutionTwo resistors of 500 Omega and 300 Omega are connected in series with a battery of emf 20 V.A voltmeter of resistance 500 Omega is used to measure the p.d across the 500 Omega resistor. The error in the measurement is.
View SolutionA high impedance AC voltmeter is connected in turn across the inductor, the capacitor and the resistor in a series circuit having an AC source of 100 V (rms) and gives the same reading in volts in each case. This reading is:
View SolutionA fresh dry cell of 1.5 volt and two resistors of 10kΩ each are connected in series. An analog voltmeter measures a voltage of 0.5 volt across each of the resistor. A 100μF capacitor is fully charged using the same source. The same voltmeter is now used to measure the voltage across It. The initial value of the current and the time in which the voltmeter reading falls to 0.5 volt are respectively.
View Solution50Ω and 100Ω resistors are connected in series. This connection is connected with a battery of 24 volts. When a voltmeter of 100Ω resistance is connected across 100Ω resistor, then the reading of the voltmeter will be
View SolutionA 600Ω resistor and a 400Ω resistor are connected in series across a 90-volt line. A voltmeter acros the 600Ω resistor reads 45V. What is the value of the voltmeter resistance? If the same voltmeter is connected across the 400Ω resistor, what will be its reading?
View Solution1.5 वोल्ट का एक आदर्श सेल 100Ω तथा 200Ω के प्रतिरोधों के श्रेणी संयोजन में धारा भेजता हैं जैसा कि चित्र में प्रदर्शित हैं। परिपथ में 100Ω के प्रतिरोध पर वोल्टता नापने के लिए 1000Ω प्रतिरोध को वोल्टमीटर चित्रानुसार लगा दिया जाता हैं। वोल्टमीटर का पाठ्यांक ज्ञात कीजिए।
View SolutionTwo resistors 4 Omega and 800 Omega are connected in series with a 6V battery. The potential difference measured by voltmeter of 10kOmega across 400 Omega resistor is
View SolutionAn inductor, a capacitor and a resistor are connected in series to an a.c. supply. When measured with an a.c. voltmeter, the potential difference across the inductor, capacitor and resistor are respectively 90 volt, 60 volt and 40 volt. Then the supply voltage is
View Solution

