A plane mirror coincides with a plane having equation x = 3. A particle is moving along a line with direction rations 3,4,5. If speed of the particle is √2, the velocity of its image is
The correct Answer is:D
To solve the problem, we need to determine the velocity of the image of a particle moving in the presence of a plane mirror located at x=3.
1. Identify the Direction Ratios and Speed:
The direction ratios of the particle's motion are given as 3,4,5 and its speed is √2.
2. Calculate the Velocity Components:
The velocity vector →v of the particle can be expressed using the direction ratios and speed. The components of the velocity in the x,y,z directions are given by:
→v=(3√32+42+52⋅√2,4√32+42+52⋅√2,5√32+42+52⋅√2)
First, we calculate the magnitude of the direction ratios:
√32+42+52=√9+16+25=√50=5√2
Thus, the components of the velocity become:
→v=(35√2⋅√2,45√2⋅√2,55√2⋅√2)=(35,45,1)
3. Determine the Effect of the Mirror:
The mirror is located at x=3. When a particle's image is formed in a plane mirror, the component of the velocity that is perpendicular to the mirror (the x-component) will reverse its direction, while the components parallel to the mirror (the y and z-components) will remain unchanged.
4. Calculate the Image Velocity:
The original velocity vector is:
→v=(35,45,1)
The image velocity →vimage will have the x-component inverted:
→vimage=(−35,45,1)
5. Final Result:
The velocity of the image of the particle is:
→vimage=(−35,45,1)
The direction ratios of the particle's motion are given as 3,4,5 and its speed is √2.
The velocity vector →v of the particle can be expressed using the direction ratios and speed. The components of the velocity in the x,y,z directions are given by:
→v=(3√32+42+52⋅√2,4√32+42+52⋅√2,5√32+42+52⋅√2)
First, we calculate the magnitude of the direction ratios:
√32+42+52=√9+16+25=√50=5√2
Thus, the components of the velocity become:
→v=(35√2⋅√2,45√2⋅√2,55√2⋅√2)=(35,45,1)
The mirror is located at x=3. When a particle's image is formed in a plane mirror, the component of the velocity that is perpendicular to the mirror (the x-component) will reverse its direction, while the components parallel to the mirror (the y and z-components) will remain unchanged.
The original velocity vector is:
→v=(35,45,1)
The image velocity →vimage will have the x-component inverted:
→vimage=(−35,45,1)
The velocity of the image of the particle is:
→vimage=(−35,45,1)
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.57
Explore 8 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.58
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.55
Explore 8 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
At any instant, the velocity and acceleration of a particle moving along a straight line are v and a. The speed of the particle is increasing if
View SolutionLet v and a be the instantaneous velocity and acceleration of a particle moving in a plane. Then rate of change of speed dvdt of the particle is equal to
View SolutionThe coordinates of a particle moving in XY-plane very with time as x=4t2,y=2t. The locus of the particle is
View SolutionThe x-t graph of a particle moving along a straight line is shown in figure

The speed-time graph of the particle is correctly shown by
View SolutionThe acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
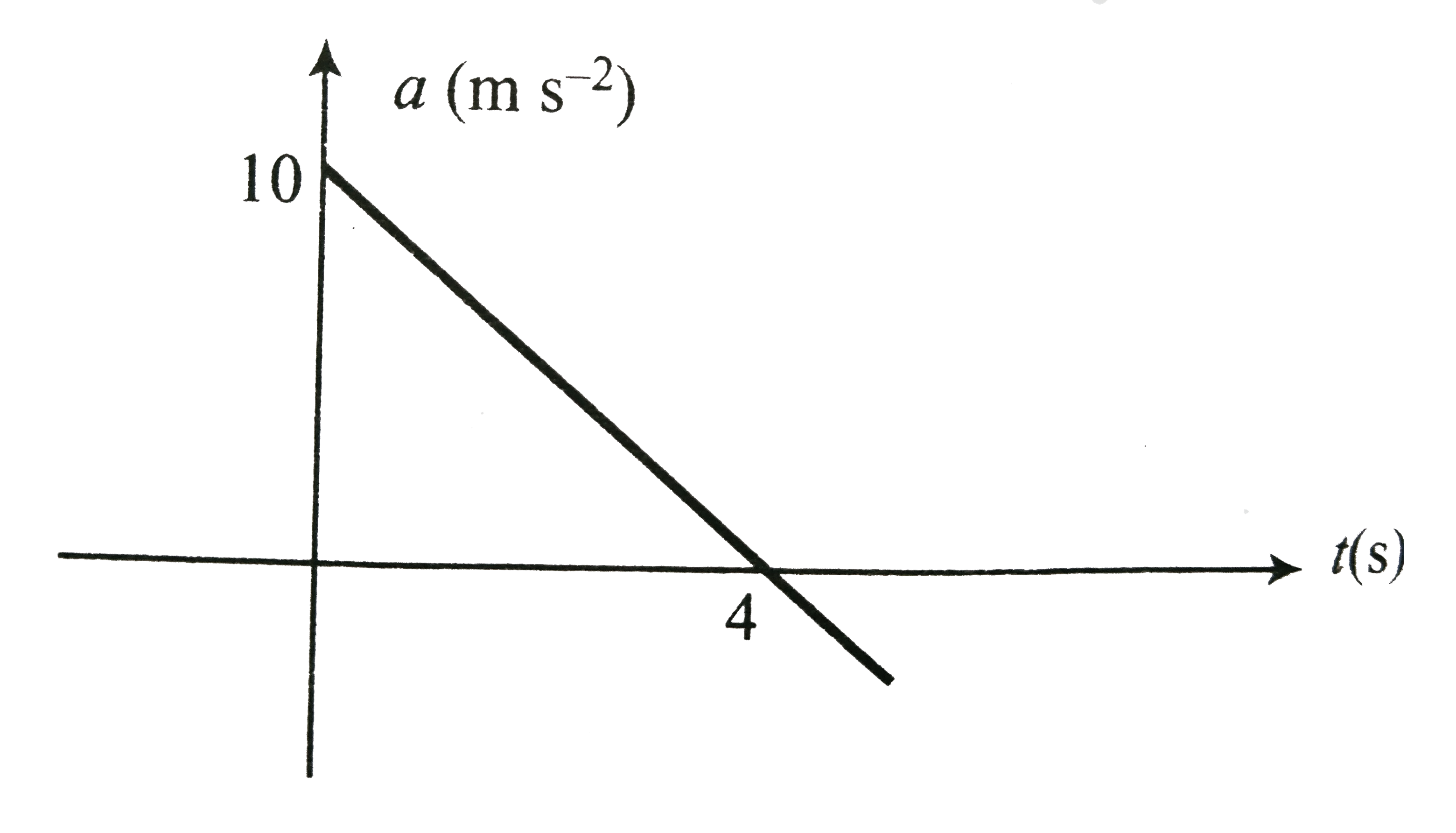 .
.
View SolutionThe acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
 .
.
View SolutionA particle is moving in x-y plane as shown in the figure. Angular velocity of the particle with respect to the origin is
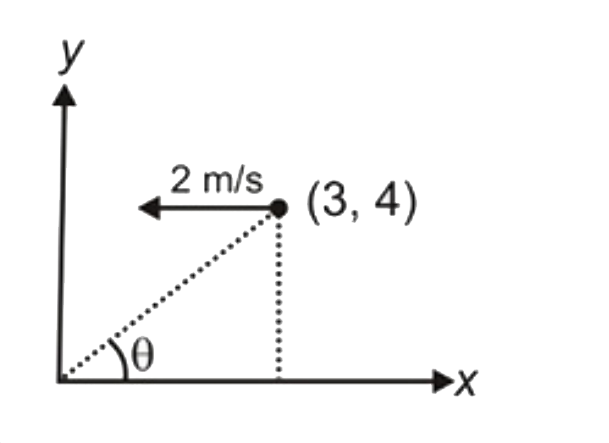
View SolutionPosition-time graph for a particle moving along x− direction is as shown in the figure. Average speed of the particle from t=0 to t=4 is :

View SolutionThe reflecting surface of a plane mirror is vertical. A particle is projected in a vertical plane which is also perpendicular to the mirror. The initial speed of the particle is 10m/s and the angle of projection is 60∘ from the normal of the mirror. The point of projection is at a distance 5m from the mirror. The particle moves towards the mirror. Just before the particle touches the mirror, the velocity of approach of the particle and the image is:
View SolutionA particle is moving along x-axis. Its velocity v with x co-ordinate is varying as v=√x. Then
View Solution
