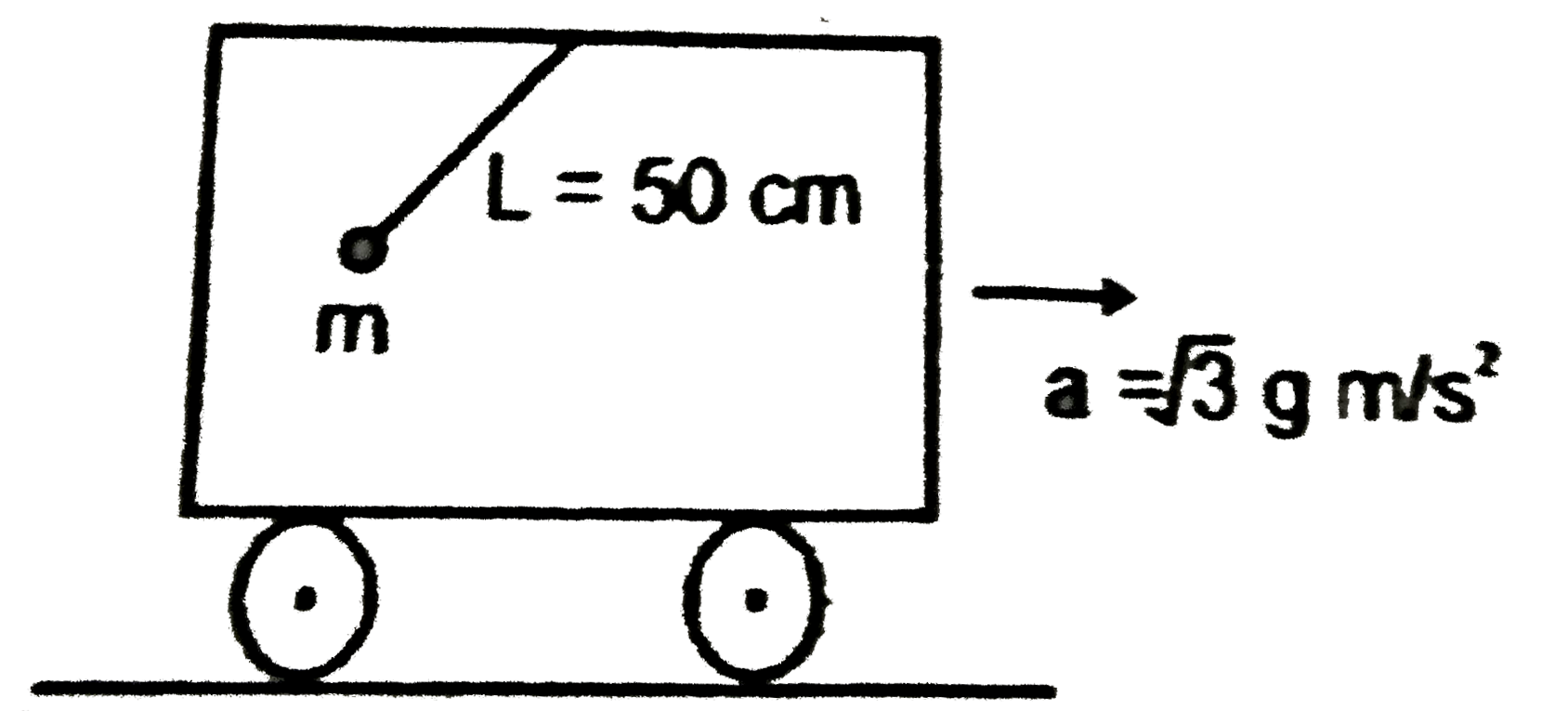
A simple pendulum 50cm long is suspended from the roof of a cart accelerating in the horizontal direction with constant acceleration √3gm/s2. The period of small oscillations of the pendulum about its equailibrium position is (g=π2m/s2):
1.0 sec
√2sec
1.53 sec
1.68 sec
The correct Answer is:A
With respect to the cart, equilibrium position of the pendulum is shown.
If displaced by small angle θ from this positon, then it will execute SHM about this equilibrium position, time period of which is given by
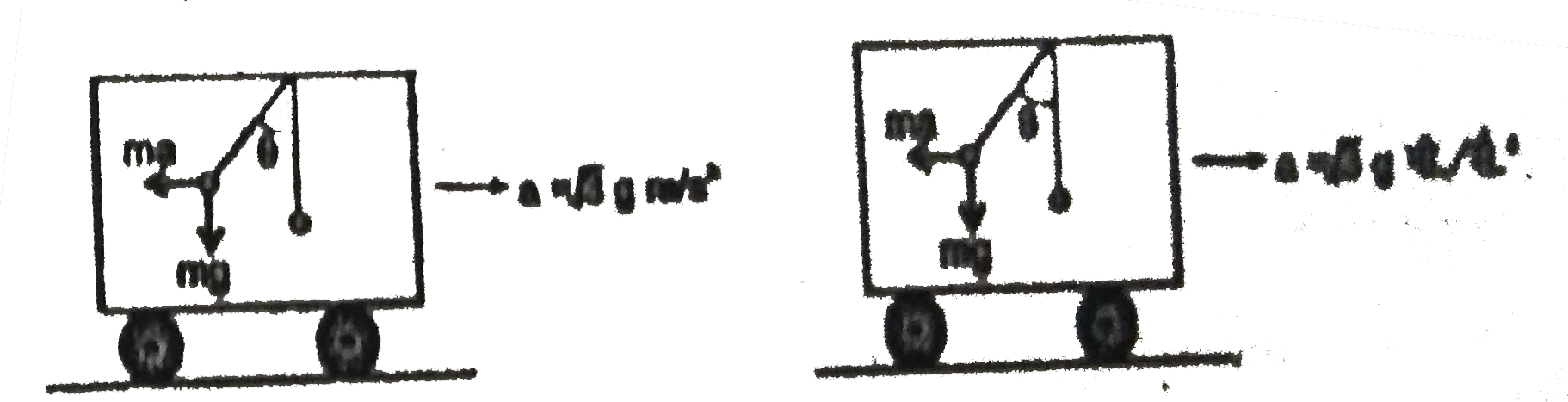
T=2π√Lgeff,geff=√g2+(√3g2)⇒geff=2g⇒T=1.0 second
Topper's Solved these Questions
Similar Questions
The pressure P, volume V and temperature T of a gas in the jar A and the othere gas in the jar B at pressure 2P, volume V/4 and temperature 2T, then the ratio of the number of molecules in the jar A and B will be :
View SolutionIn the situation shown in figure, find the velocity of image.

View SolutionA seconds pendulum is suspended from the ceiling of a trolley moving horizontally with an acceleration of 4 m//s^(2) . Its period of oscillation is
View SolutionA simple pendulum 50cm long is suspended from the roof of a acceleration in the horizontal direction with constant acceleration √3gm/s−1. The period of small oscillations of the pendulum about its equilibrium position is (g=π2m/s2) ltbRgt

View Solutionएक स्थिर लिफ्ट में छत से लटके किसी सरल लोलक का आवर्तकाल 2 सेकंड है । यदि लिफ्ट ऊपर की ओर 2 मी / से2 के त्वरण से उठती है, तो सरल लोलक का आवर्तकाल होगा (g = 10 मी / से^(2))
View SolutionA simple pendulum of length 1 m is freely suspended from the ceiling of an elevator. The time period of small oscillations as the elevator moves up with an acceleration of 2m/s2 is (use g=10m/s2)
View SolutionA simple pendulum of length 1 m is freely suspended from the ceiling of an elevator the time period of small oscollations as the elevator moves up with an acceleration of 2m//s ^2 is ( use g=10 m//s ^2)
View SolutionA simple pendulum is suspended from the roof of a car moving horizontally with an acceleration of 10m⋅s−2 . What will be the angle made by the pendulum in its equilibrium position with the vertical ? [g=10m⋅s−2]
View Solutionएक स्थिर लिफ्ट की छत से टंगे हुए सरल लोलक का दोलनकाल T है। यदि parinaami त्वरण g/4 हो जाता है , तो सरल लोलक का दोलनकाल होगा।
View SolutionA trolley moves in horizontal direction with an acceleration a. A simple pendulum of length l is suspended from the roof of the trolley. The time period of the pendulum will be
View SolutionA simple pendulum of length 1 m is freely suspended from the ceiling of an elevator the time period of small oscollations as the elevator moves up with an acceleration of 2m/s2 is ( use g=10m/s2)
View SolutionA simple pendulum 4 m long swing with an amplitude of 0.2 m. What is its acceleration at the ends of its path? (g=10m/s2)

View SolutionA simple pendulum is of length 50cm. Find its time period and frequency of oscillation. (g=9.8m/s2).
View SolutionA simple pendulum is hanging from the roof of a trolley which is moving horizontally with acceleration g. If length of the string is L and mass of the bob is m, then time period of oscillation is
View SolutionA simple pendulum of length 1 m is freely suspended from the ceiling of an elevator. The time period of small oscillations as the elevator moves up with an acceleration of 2m//s^2 is (use g=10 m//s^2 )
View SolutionA seconds pendulum is suspended from the ceiling of a trolley moving horizontally with an acceleration of 4m/s2 . Its period of oscillation is
View Solution

