Three point masses are attached by light inextensible strings of various lengths to a point O on the ceiling. All of the masses swing round in horizontal circles of various radii with the same angular frequency ω (one such circle is drawn in the shown figure.) Then pick up the correct statement.
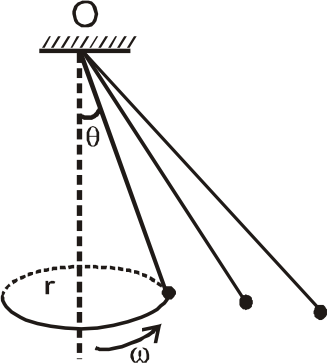
The vertical depth of each mass below point of suspension from ceilling is different
the radius of horizontal circular path of eachmass is same
all masses revolve in the same horizontal plane
all the particles must have same mass.
The correct Answer is:C
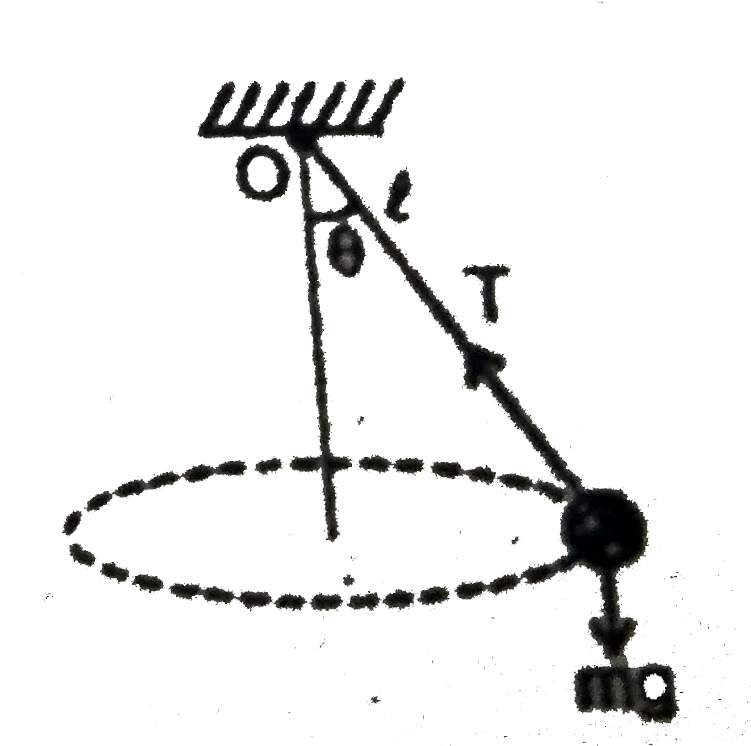
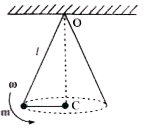
For conical pendulum l , mass m moving
along horizontal circle is as shown
Tcosθ=mg.....(1)
Tsinθ=mω2lsinθ.....(2)
From equation (1) and equation (2), lcosθ=gω2
lcosθ is the vertical distance of below O point of suspension. hence if ω of all three pendulum are same, they small revolve in same horizontal plane.
Alternate.
If we remember that time period T of conical pendulum is
T=2π√Lg where L is the vertical path of bob below point of suspension. If T is same for three pendulum
even L shall be also same. hence all three particles shall revolve in same horizontal plane
Topper's Solved these Questions
Similar Questions
A ball of density d is dropped onto a horizontal solid surface. It bounces elastically from the surface and returns to its original position in a time t1. Next, the ball is relasesed and it falls through the same height before striking the surface of a liquid of density dL.
(a) If d<dL, obtain an expression ( in terms of d,t1 and dL) for the time t2 the ball takes to come back to the position from which it was released.
(b) Is the motion of the ball simple harmonic?
(c ) If d=dL how does the speed of the ball depend on its depth inside the liquid? Neglect all frictional and other dissipative force. Assume the depth of the liquid to be large.
View SolutionAn electron is placed just in the middle between two long fixed line charges of charge density +λ each. The wires are in the xy plane (do not consider gravity)
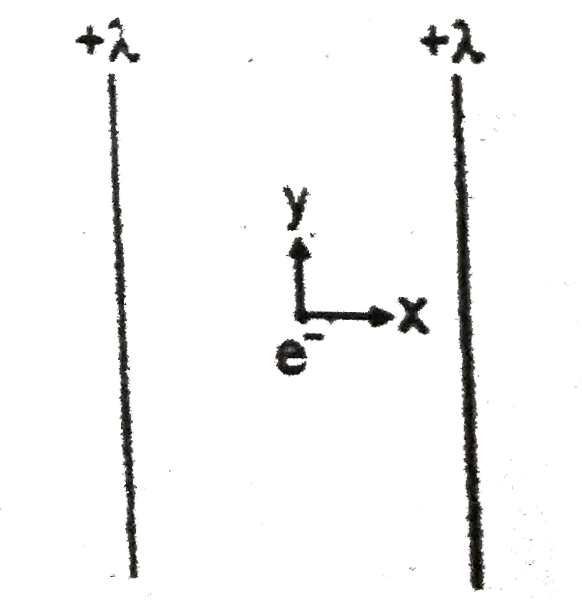
View SolutionA bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
View SolutionThree point masses are attached by light inextensible strings of various lengths to a point O on the ceiling. All of the masses swing round in horizontal circles of various radii with the same angular frequency ω (one such circle is drawn in the shown figure.) Then pick up the correct statement.

View SolutionA small ball of mass m suspended from the celling at a point O by a thread of length l moves along a horizontal circle with a constant angular velocity omega . .
View SolutionA block of mass 2m is attached to a string of length L=5m. The block is released when the string is horizontal , it picks up a particle of 2m kept at rest at the lowest point. The maximum height attached by the combined mass is
View SolutionA bob of mass 2kg is suspended from point O of a core with an inextensible string strinng of length sqrt(3)m . It is moving in horizontal circle over the surface of cone as shown in the figure. Then :(g=10m//s^(2))
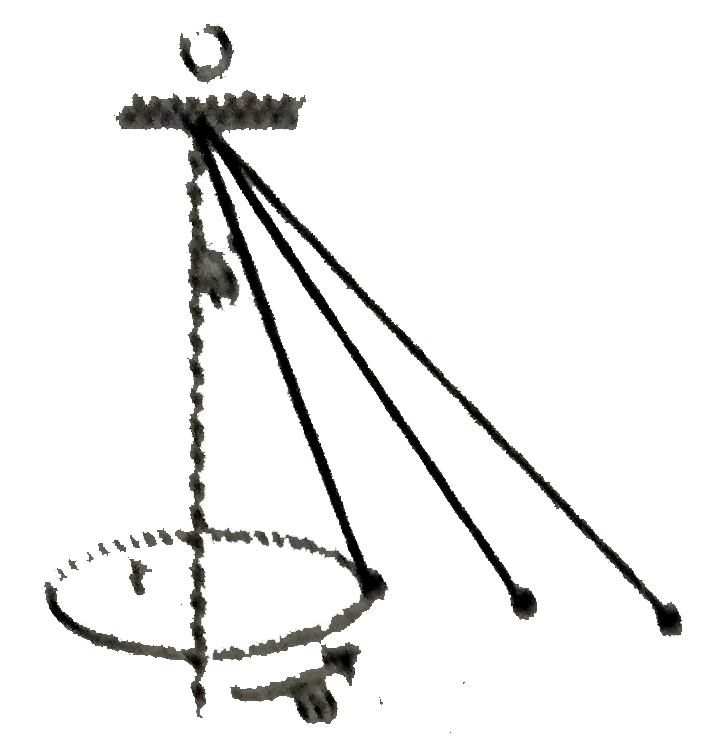
View SolutionThree masses of small size are attached by light inextensible strings of various lengths to a point O on the ceiling. All of the masses swing round in horizontal circles of various radii with the same angular frequency ω (one such circle is drawn in the shown figure.) Then pick up the correct statement.
View SolutionThree balls each of mass 1 kg are attached with three strings each of length 1 m as shown in figure. They are rotated in a horizontal circle with angular velocity ω=4rad s−1 about point O. Match the following columns.
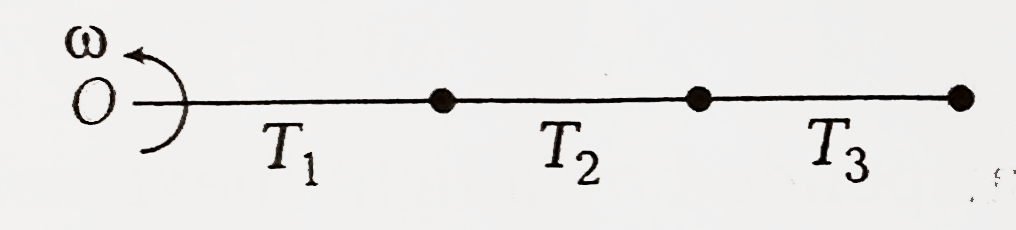
View SolutionA particle of mass m attached to an inextensible light string is moving in a vertical circle of radius r. The critical velocity at the highest point is v_( 0) to complete the vertical circle. The tension in the string when it becomes horizontal is
View SolutionA bob of mass m attached to an inextensible string of length l is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed omega rad/s about the vertical support. About the point of suspension
View SolutionA bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
View SolutionA Small ball of mass m suspended from the ceiling at a point O by a thread of length l moves along a horizontal circle with a constant angular velocity ω. Which of the following statements(s) is/are correct ?
View SolutionThree balls each of mass 1 kg are attached with three strings each of length 1 m as shown in figure. They are rotated in a horizontal circle with angular velocity omega=4"rad s"^(-1) about point O. Match the following columns.
View SolutionThree balls each of mass 1 kg are attached with three strings each of length 1 m as shown in figure. They are rotated in a horizontal circle with angular velocity ω=4rad s−1 about point O.find the tensions .
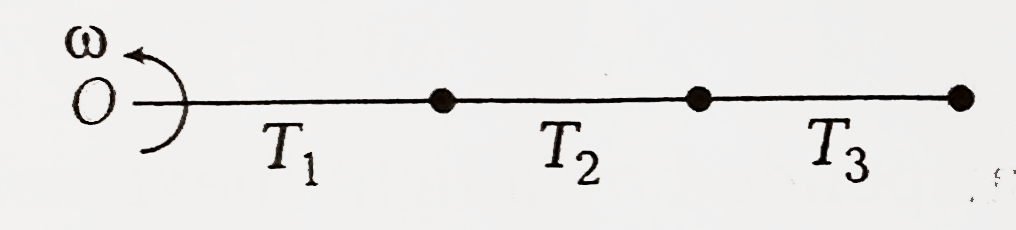
View SolutionA bob of mass m attached to an inextensible string of length l is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω rad/s about the vertical. About the point of suspension
View Solution

