Statement 1: A pendulum made of an insulated rigid massless rod of length l is attached to a small sphere of mass m and charge q. The pendulum is undergoinng oscillations of small amplitude having time period T. Now a uniform horizontal magnetic field →B out of plane of page is switched on. As a result of this change, the time period of oscillations does not change.
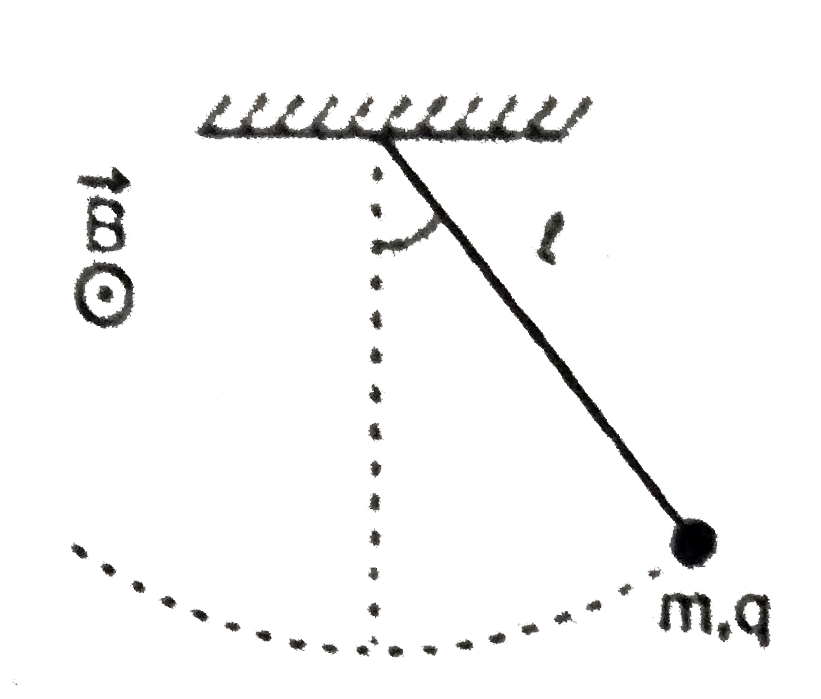
Statement 2: A force acting along the string on the bob of a simple pendulum (such that tension in string is never zero) does not produce any restoring torque on the bob about the hinge.
Statement-1 is true, Statement-2: is true, Statement-2 is a correct explanation for Statement-1.
Statement-1 is true, Statement-2: is true, Statement-2 is NOT a correct explanation for Statement-1.
Statement-1 is true but statement-2 is false
Statement-1 is false, Statement-2 is true
The correct Answer is:A
The magnetic force on bob does not produced any restoring torque on bob about the hinge. Hence this force has no effect on time period of oscillation. Therefore both statements are correct and statement-2 is the correct explanation.
Topper's Solved these Questions
Similar Questions
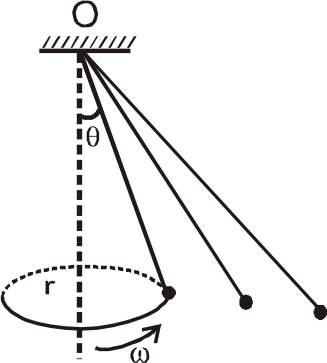
Three point masses are attached by light inextensible strings of various lengths to a point O on the ceiling. All of the masses swing round in horizontal circles of various radii with the same angular frequency ω (one such circle is drawn in the shown figure.) Then pick up the correct statement.
View SolutionOne mole of an ideal monoatomic gas is mixed with one mole of an equimolar mixture of monoatomic and diatomic ideal gases. Find the value of λ=(CPCv) for the final mixture
View SolutionA uniform rod of length l is suspended by end and is made to undego small oscillations. Find the length of the simple pendulum having the time period equal to that of the rod.
View SolutionA small bob attached to a light inextensible thread of length l has a periodic time T when allowed to vibrate as a simple pendulum. The thread is now suspended from a fixed end O of a vertical rigid rod of length 3l//4 . If now the pendulum performs periodic oscillations in this arrangement, the periodic time will be
View SolutionA small bob attached to a light inextensible thread of length l has a periodic time T when
allowed to vibrate as a simple pendulum. The thread is now suspended from a fixed end O of a vertical rigid rod of length 3l4 (as in figure). If now the pendulum performs periodic oscillations in this arrangement, the periodic time will be-
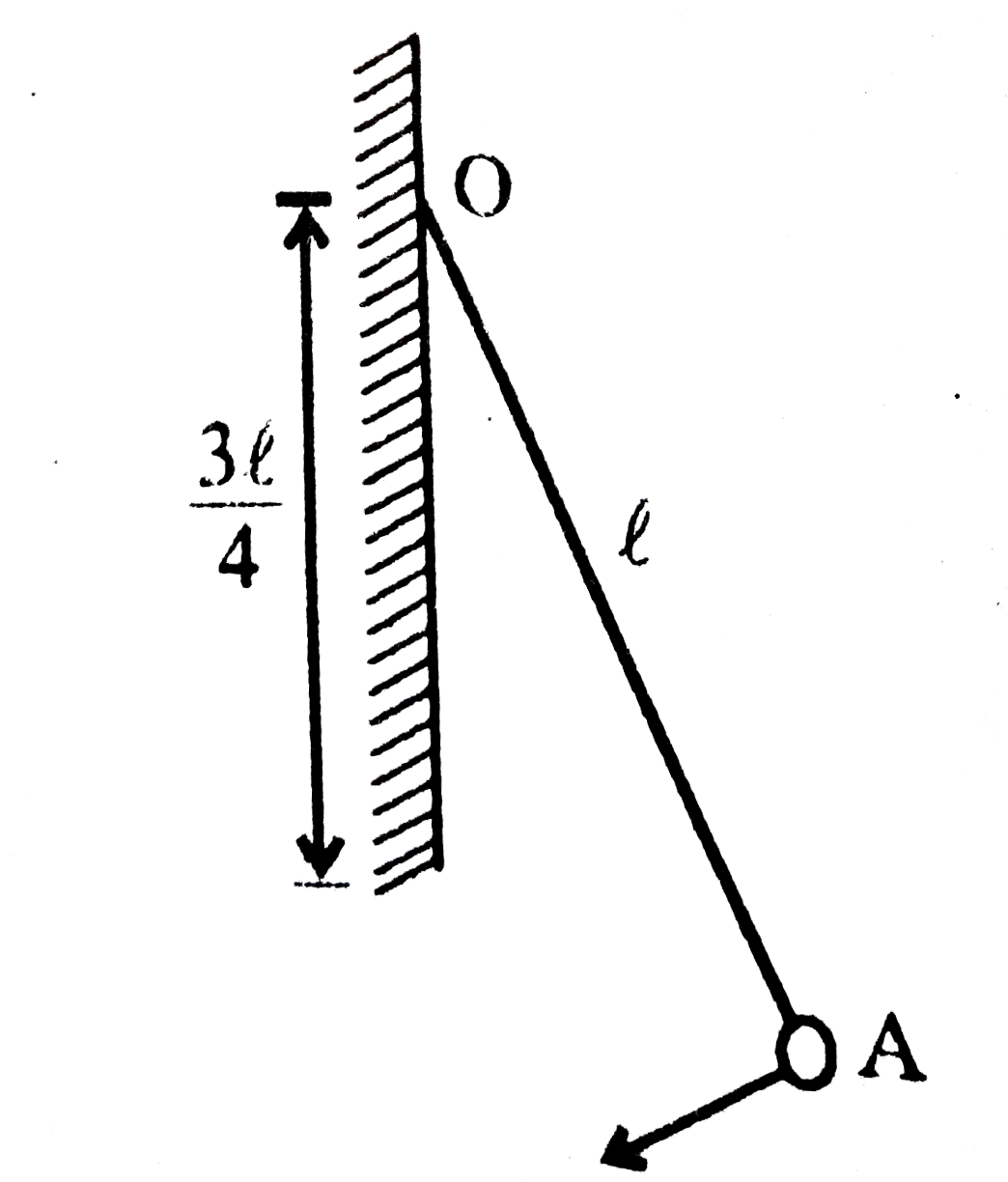
View SolutionStatement 1: A pendulum made of an insulated rigid massless rod of length l is attached to a small sphere of mass m and charge q. The pendulum is undergoinng oscillations of small amplitude having time period T. Now a uniform horizontal magnetic field vec B out of plane of page is switched on. As a result of this change, the time period of oscillations does not change. Statement 2: A force acting along the string on the bob of a simple pendulum (such that tension in string is never zero) does not produce any restoring torque on the bob about the hinge.
View SolutionA simple pendulum oscillating with a small amplitude has a time period of T = 1.0s . A horizontal thin rod is now placed beneath the point of suspension at a distance equal to half the length of the pendulum. The string collides with the rod once in each oscillation and there is no loss of energy in such collisions. Find the new time period T of the pendulum
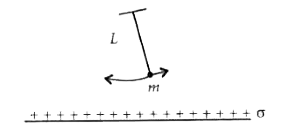
View SolutionA pendulum has a bob of mass m carrying a positive charge q. Length of the pendulum string is L. Beneath the pendulum there is a large horizontal dielectric sheet of charge having uniform surface charge density of sigma C//m^2 . [figure (i)] (a) Find the time period of small oscillations for the pendulum (b) Now the dielectric sheet of charge is tilted so as to make an angle beta with horizontal. Find the angle (a) that the thread makes with vertical in equilibrium position. Find time period of small oscillations in this case. [figure (ii)]
View SolutionA simple pendulum has time period T. Charges are now fixed at the point of suspension of the pendulum and on the bob. If the pendulum continues to oscillate, its time period will now be
View Solutionलम्बाई l तथा द्रव्यमान m के गोलक से बने हुआ एक सरल लोलक का दोलन-अवधि काल T है । यदि लोलक की लम्बाई को 4 तक बढ़ाते हैं तथा गोलक के द्रव्यमान को त2m क बढ़ाते है, तो नया दोलन - अवधि काल निम्नलिखित में से कौन-सा है ?
View SolutionA simple pendulum with charged bob is oscillating with time period T and let theta be the angular displacement. If the uniform magnetic field is switched ON in a direction perpendicular to the plane of oscillation then
View SolutionA simple pendulum has time period T. A uniform rod, whose length is the same as that of the pendulum, undergoes small oscillations about its upper end. Its time period of oscillation will be -
View SolutionA uniform rod of length 1.8 m suspended by an end is made to undergo small oscillations. Find the length of the simple pendulum having the mass and time period equal to that of the rod.
View SolutionA simple pendulum with charged bob is oscillating with time period T and let θ be the angular displacement. If the uniform magnetic field is switched ON in a direction perpendicular to the plane of oscillation then
View SolutionA simple pendulum with charged bob is oscillating with time period T and let θ be the angular displacement. If the uniform magnetic field is switched ON in a direction perpendicular to the plane of oscillation then
View SolutionThe bob of a pendulum of mass 'm' suspended by an inextensible string of length L as shown in the figure carries a small charge 'q' . An infinite horizontal plane conductor with uniform surface charge density sigma1 is placed below it . What will be the time period of the pendulum for small amplitude oscillations ?
View Solution

